| VADEMECUM REMER |
| Conocimientos de topografía y cartografía |
![]() Geodesia
Geodesia
![]() Topografía
Topografía
![]() Taquimetría
Taquimetría
![]() Clasificación del terreno
Clasificación del terreno
![]() Accidentes del terreno
Accidentes del terreno
![]() Cartografía
Cartografía
![]() Cartas
Cartas
![]() Mapas
Mapas
![]() Planos
Planos
![]() Lectura de planos
Lectura de planos
![]() Escala
Escala
![]() Escala gráfica de un plano
Escala gráfica de un plano
![]() Ejemplo de utilización de la escala gráfica
Ejemplo de utilización de la escala gráfica
![]() Orientación
Orientación
![]() Signos convencionales
Signos convencionales
![]() Curvas de nivel
Curvas de nivel
![]() Características de las curvas de nivel
Características de las curvas de nivel
![]() Otro sistema de representación del relieve. Planos acotados
Otro sistema de representación del relieve. Planos acotados
![]() Pendientes
Pendientes
![]() Laderas y cuestas
Laderas y cuestas
![]() Perfiles
Perfiles
![]() Entrantes y salientes
Entrantes y salientes
![]() Cerros, valles y puertos
Cerros, valles y puertos
![]() Medidas angulares
Medidas angulares
![]() Distancias que se consideran en el terreno y en el plano
Distancias que se consideran en el terreno y en el plano
![]() Coordenadas geográficas
Coordenadas geográficas
![]() Identificación de la longitud y la latitud
Identificación de la longitud y la latitud
![]() Coordenadas de las capitales de provincia de España. (por el meridiano de Greenwich)
Coordenadas de las capitales de provincia de España. (por el meridiano de Greenwich)
| Geodesia |
Etimológicamente la palabra geodesia procede del griego "geo" = tierra y "daio" = dividir. Es la ciencia que estudia, por medios matemáticos, la forma y dimensiones de la Tierra y para conseguirlo se eligen en la superficie, objeto de estudio, puntos distribuidos por toda ella denominados geodésicos de cuya posición se deduce la forma de un territorio o de todo el globo.
Para situar estos puntos, es preciso referirlos a una superficie que podría ser real o arbitraria. Si se prolongase por debajo de los continentes el nivel medio de los mares en calma se obtendría una superficie equipotencial, denominada geoide de forma irregular que aproximadamente se adapta a un elipsoide de revolución ligeramente achatado por los polos.
La esfericidad terrestre ya se conocía por los griegos. Así por ejemplo, en el siglo II a.C., Eratostones dedujo la longitud del meridiano terrestre en 250.000 estadios, es decir, unos 40.000.000 de metros, pero consideraban a la tierra inmóvil, situada en el centro del Universo.

Sin embargo, hasta los descubrimientos geográficos de finales de la Edad Media y los estudios astronómicos de Copérnico y Galileo, las representaciones de la Tierra se realizaban sin tener en cuenta la esfericidad terrestre.
| Topografía |
Etimológicamente la palabra topografía procede del griego "topo" = lugar, y "grafos" = dibujo. Es la ciencia que con el auxilio de las matemáticas nos ayuda a representar gráficamente (mediante un dibujo), un terreno o lugar determinado, con todos sus accidentes y particularidades naturales o artificiales de su superficie.
En las proyecciones topográficas se distinguen dos partes: Planimetría y Altimetría.
Planimetría es la proyección de cada punto interesante del terreno sobre un plano horizontal, tomado como referencia.
Altimetría, es la determinación de las cotas de los diferentes puntos del terreno, con respecto al plano horizontal de comparación, el cual, aunque puede ser tomado a una altura arbitraria, en general se relaciona con el plano horizontal teórico formado por el nivel del mar en Alicante, en el caso de España.
| Taquimetría |
Es la parte de la topografía que se ocupa de los procedimientos existentes para confeccionar o levantar un plano por medio de diversos instrumentos, denominadas en general teodolitos, taquímetros, distanciómetros. Todos ellos se basan en la medición de distancias, alturas y ángulos de los distintos puntos del terreno, en relación con el punto desde donde se observan, llamado "estación".
Se denomina "levantamiento topográfico", al conjunto de operaciones realizadas sobre el terreno, con los instrumentos adecuados, que posteriormente nos permitirá la confección del Plano de ese lugar o zona. Estas operaciones tienen como finalidad la determinación de datos numéricos suficientes para confeccionar el plano. Como es preciso realizarlas sobre el propio terreno, se las denomina como "trabajo de campo".
Se denomina "levantamiento del plano", al conjunto de operaciones realizadas con los datos obtenidos en el levantamiento topográfico, que nos permitan confeccionar un dibujo a escala o plano del lugar que se considera. Como estas se hacen en el estudio u oficina, se las denomina como "trabajo de gabinete".
| Clasificación del terreno |
Para representar un terreno y comprender su representación debemos conocer primero su clasificación dependiendo de su estructura, su naturaleza o su producción.
Terreno llano |
Es aquel que presenta pendientes suaves. |
Terreno ondulado |
Es aquel formado por elevaciones y depresiones de pequeña importancia. Son pendientes que permiten el acceso en todas las direcciones. |
Terreno montañoso |
Tiene elevaciones y depresiones de mayor importancia, de no fácil acceso, existiendo puntos por los que se puede atravesar con facilidad. |
Terreno escarpado |
Presenta bruscos cambios de pendiente y cortados frecuentes. Sus laderas son abruptas y a veces inaccesibles. |
Según la naturaleza lo clasificaremos en:
| Terreno compacto | Es el que presenta un suelo firme. |
| Terreno pedregoso | El que presenta en zonas o en su totalidad piedras o terreno suelto. |
| Terreno blando | El que presenta poca consistencia en su terreno. |
| Terreno arenoso | El que presenta amplias zonas de arena y dunas (desiertos). |
| Terreno pantanoso | Es la zona de terreno donde el agua por no correr libremente se estanca formando cieno y barro. |
Según su producción lo clasificaremos en:
| Terreno despejado | El que no presenta vegetación a destacar o la tiene escasa y de poca altura. |
| Terreno abierto | El que presenta zonas de labor y cultivos o bien monte bajo, alto o bosques. |
| Accidentes del terreno |
Los principales accidentes del terreno son los siguientes:
| Monte | Gran elevación del terreno que destaca sobre el que le rodea, su parte más alta es la cima. Si esta es alargada se denomina cresta y si es puntiaguda se denomina pico. |
| Mogote | Pequeña elevación del terreno, respecto al que le rodea. Si tiene forma alargada se llama loma. Cuando sus laderas tienen mucha pendiente se le denomina cerro y si esta aislado se llama otero. |
| Laderas o vertientes | Son las superficies laterales de cada elevación. |
| Vaguada | Es la intersección por su parte inferior de dos vertientes o laderas opuestas. |
| Barranco | Es una vaguada cuyas vertientes presentan terreno escarpado. |
| Collado | Es una depresión entre dos divisorias, si es de fácil acceso se denomina puerto. Si es largo y estrecho, garganta y si es muy profundo cañón o desfiladero. |
| Valle | Es un terreno mas o menos llano, comprendido entre dos divisorias, por el cual normalmente discurre un curso de agua. |
| Río | Es una corriente de agua de mayor o menor importancia. El terreno por donde discurren sus aguas se denomina cauce o lecho. Cuando solo circula en tiempos de lluvias se llama torrentera. |
| Confluencia | Es el punto de unión de dos cursos de agua. |
| Vado | Es el lugar de un río o arroyo por donde se puede cruzar a pie. |
| Hoya | Es una depresión de terreno respecto al que le rodea. Si la hoya tiene agua permanente y es de grandes dimensiones, se llama lago. Y si es de pequeñas dimensiones se llama charca. |
| Costa | Es la franja de terreno colindante con el mar. Si es baja y arenosa se llama playa. Y si es abrupta y escarpada se llama acantilado. |
| Cartografía |
Es el conjunto de estudios y operaciones científicas y técnicas que intervienen en la formación o análisis de mapas, modelos en relieve o globos, que representan la Tierra, o parte de ella o cualquier parte del Universo.
| Cartas |
Son representaciones sobre un plano, de grandes extensiones de la superficie terrestre, en los que figuran islas, costas, mares, profundidades, alturas, etc., obtenidos por procedimientos especiales, debidos a la curvatura de la Tierra.
| Mapas |
Son representaciones de grandes extensiones de un territorio, obtenidas por procedimientos geodésicos.
Según lo que se pretende informar con el mapa, pueden agruparse en dos clases:
- Por su extensión
- Por su finalidad
Por su extensión:
| Mapamundi | Cuando esta representada toda la superficie terrestre. |
| Continental | Cuando el mapa representa uno de los continentes. |
| Nacional | Cuando lo que se representa es una nación. |
| Autonómico | Cuando lo que se representa es una Comunidad Autónoma. |
| Provincial | Cuando se representa una provincia. |
| Comarcal | Cuando se refiere a una comarca. |
| Local | Cuando lo es de una localidad o su término municipal. |
Por su finalidad:
| Mapas topográficos | Mapas físicos | En los que se representan aspectos físicos del suelo, como los montes, ríos y demás accidentes geográficos. |
| Mapas temáticos | Mapas políticos | Cuando se representan las divisiones administrativas realizadas por el hombre, tales como fronteras, limites provinciales, y demás divisiones administrativas. |
| Mapas económicos | Los que representan los diversos aspectos económicos, areas y zonas de producción de productos, minería, factorías, industrias, etc. |
|
| Mapas geológicos | Cuando se refieren a la geología del suelo. |
|
| Mapas de población | Cuando se tratan de la distribución de la población, razas, densidades de la población, agrupaciones urbanas o rurales, etc. |
|
| Mapas climáticos | Los que nos representan gráficamente la climatología u otros accidentes meteorológicos. |
|
| Mapas de catástrofes | Aquellos que se ocupan de representar gráficamente las zonas de sequías, incendios, inundaciones, accidentes de tráfico, etc. |
|
| Otros mapas | Confeccionados en función de lo que se pretende informar. |
| Planos |
Son las representaciones de una pequeña porción de la superficie terrestre, que solo precisa de operaciones topográficas, para la toma de datos, prescindiendo de la curvatura de la Tierra, en su formación.
| Lectura de planos |
Leer un plano es saber interpretarlo exactamente, de acuerdo con unas normas preestablecidas, de tal modo que no sea preciso situarse sobre el propio terreno, para llegar a un conocimiento del mismo, tanto mas profundo, cuanto mayor sean los conocimientos básicos que se posean. Es decir, leer un plano, puede suponer llegar a adquirir todos y cada uno de los datos o conocimientos que el autor del mismo vertió en su confección.
Para leerlo, en principio es indispensable unos conocimientos básicos y claros acerca de los conceptos siguientes: escala, orientación, signos convencionales, curvas de nivel y unos elementales principios de aritmética y geometría.
| Escala |
Es el concepto fundamental en las representaciones gráficas, bien sean cartas, mapas, planos, croquis u otras gráficas.
Se define como "la relación existente entre la medida gráfica del dibujo y la real del terreno". Y se puede expresar mediante la siguiente división:
Escala = medida del plano / medida del terreno
E = P / T o E = P : T
Es indispensable que ambas medidas se expresen en la misma clase de unidades, es decir, ambas en metros (m), centímetros (cm), o bien en milímetros (mm), o cualquier otra clase de unidades que deseemos, como podrían ser otras unidades arbitrarias, tales como la longitud de un palo, palmos, pies, etc.
Veamos dos ejemplos relativos al manejo de escalas:
1. Ejemplo: Tenemos un plano a escala E = 1:10.000.
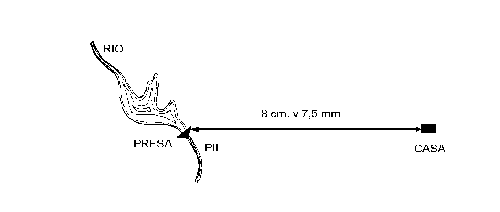
Queremos saber la distancia que existe en línea recta entre dos puntos determinados, (por ejemplo, entre la esquina de una casa y la presa de un río que hay en sus inmediaciones).
Se mide en el plano, mediante una regla la distancia entre los dos puntos, debidamente identificados.
Supongamos que la medida es de 8 cm y 7.5 mm
Expresamos dicha medición en la misma clase de unidades, por ejemplo en mm., así:
8 cm y 7.5 mm = 87.5 mm
Ahora plantearemos una "regla de tres":
(Supuesto) Si 1 mm del plano son 10.000 mm en terreno
(Pregunta) 87.5 mm del plano serán X mm en terreno
(En donde) X = 87.5 x 10.000 / 1 = 875.000 mm
Como las unidades empleadas corrientemente para medir distancias sobre el terreno son el metro o bien el kilómetro, habremos de reducir el resultado anterior a metros o bien a kilómetros, así:
875.000 mm / 1.000 mm (que son los mm que tiene 1 m), nos da: 875 m
Si queremos expresar la distancia real en km dividiremos del mismo modo por 1.000 m, que son los metros que tiene 1 km, así: 0.875 km
Por tanto, la distancia real existente entre la esquina de la casa y la presa del río antes expresada es de 875 m o bien 0.875 km.
2. Ejemplo: Tenemos un plano a escala E = 1:50.000
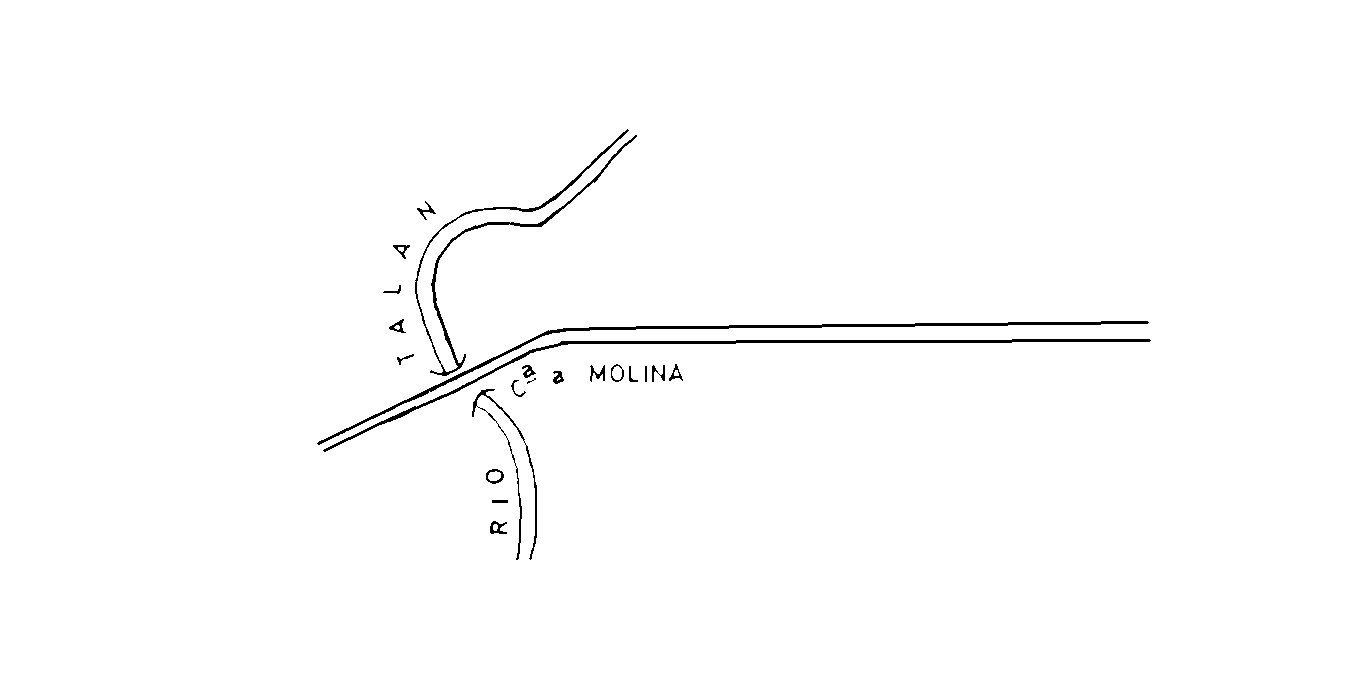
En él figura un puente sobre un río, pero no figura dibujada una cabaña que vemos que existe al borde del camino que conduce a dicho puente. Queremos situar con exactitud dicha cabaña en el plano.
Comenzaremos cerciorándonos de que el puente y el camino reales, son los que figuran dibujados en el plano.
Mediremos en el terreno la distancia que hay en línea recta y lo mas horizontalmente posible, entre el puente y la cabaña, mediante una cinta métrica. Supongamos que son 482 m.
De nuevo plantearemos una "regla de tres", así:
(Supuesto) Si 1 m del plano son 50.000 m en terreno.
(Pregunta) X m del plano serán 482 m en terreno.
(En donde) X = 482 x 1 / 50.000 = 0.00964 m x 1.000 = 9.64 mm
El punto de situación en el plano, de la cabaña, lo encontraremos trazando un arco con el compás con un radio de 9.64 mm, y en el punto de intersección con el camino será el lugar exacto de situación de la cabaña en el plano.
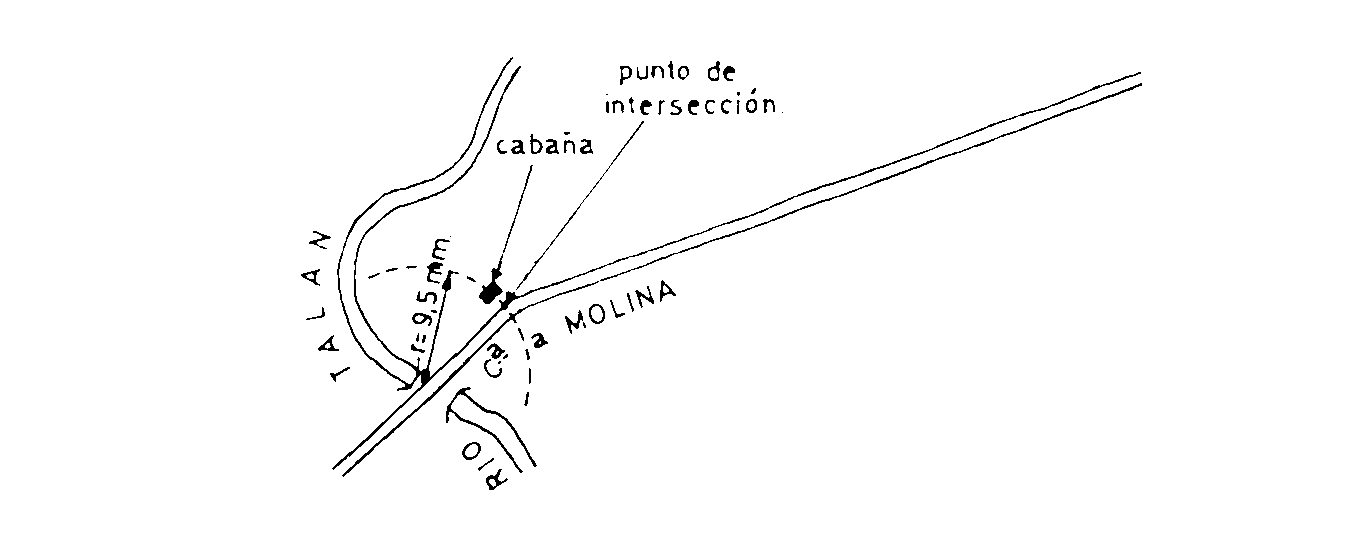
En general diremos: "Para convertir una distancia del plano en una distancia real en el terreno, hemos de multiplicar aquella por el denominador de la escala. Si es al contrario, dividiremos".
La elección de la escala para confeccionar un mapa o un plano, no es arbitraria, depende siempre de la finalidad perseguida con cada tipo de mapa, de los detalles que se han de representar en el y de las dimensiones del papel donde se dibuja en relación con la extensión de terreno que se ha medido.
Las escalas pueden ser:
- Numéricas
- Gráficas
Las escalas numéricas se expresan por una fracción o una división indicada, que para mayor sencillez, se elige siempre con numerador igual a la unidad y denominador un número cualquiera, generalmente la unidad seguida de ceros o bien el número 5 solo o seguido de ceros. Lo cual no obsta que puedan ser otros números frecuentes, tales como: 2, 20, 200, 300, etc.
Las escalas gráficas son las que aparecen construidas en el borde de casi todos los mapas y planos. Pueden ser sencillas y de transversales. Las primeras son las mas utilizadas, haciéndose uso de las segundas cuando se precisa mayor exactitud.
El modo de operar con ellas es muy sencillo. Generalmente se utilizan para mediciones rápidas o bien cuando no se dispone de regla milimétrica.
Consiste en marcar en el borde de un papel dos marcas que coincidan con los puntos del plano de los que deseamos saber su distancia real. Se llevan estas marcas sobre la escala gráfica, haciendo coincidir la marca de la izquierda con el cero de la escala y leyendo en la escala lo que nos indica la otra marca, (tal y como si estuviésemos midiendo con una regla), expresando la lectura en las mismas unidades en que venga expresada la escala gráfica.
A veces estas escalas gráficas están dibujadas de tal modo que tienen "contraescala", que es tomar hacia la izquierda del cero una de las unidades expresadas en la escala y dividida en 10 o 100 partes iguales. De este modo podemos hacer lecturas muy precisas.
| Escala gráfica de un plano |
Características más importantes de las hojas
| Serie 2V | Serie 5V | Serie L | Serie C | Serie 2C | Serie 4C | Serie 8C | |
|---|---|---|---|---|---|---|---|
| 1:10.000 | 1:25.000 | 1:50.000 | 1:100.000 | 1:200.000 | 1:400.000 | 1:800.000 | |
| Cuadrícula principal | Kilométrica | Kilométrica | Kilométrica | Kilométrica 5 | Kilométrica 10 | Kilométrica 20 | Kilométrica 100 |
| color | azul | azul | azul | azul | azul | azul | azul |
| Cuadrícula secundaria | Lambert | Lambert | Lambert | Lambert | Lambert | ||
| indicación | bordes | bordes | iniciada | iniciada | iniciada | ||
| color | verde | verde | verde | verde | verde | ||
| distancia | 1 km | 5 km | 10 km | 10 km | |||
| Cuadrícula geográfica | 1' | 1' | 5' | 10' | 15' | 30' | 1º |
| color | negro | negro | negro | negro | negro | negro | negro |
| Equidistancia de curvas | 5 m | 10 m | 20 m | 40 m | 100 m | 200 m | 400 m |
| curvas directoras | 25 m | 50 m | 100 m | 200 m | 400 m |
| Ejemplo de utilización de la escala gráfica |
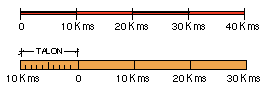
Queremos saber la distancia real, en línea recta, que existe entre las localidades de "El Espinar" y "Los Balanza" (ver líneas discontinuas).
Situamos el borde de un papel en la línea que une los dos pueblos, haciendo un trazo en cada pueblo, sobre este papel.
Este segmento lo llevamos a la escala gráfica, haciendo coincidir una de las rayas o trazos con el cero de la escala. Miramos el otro trazo y vemos que comprende 15 km y un trozo más (a-b).
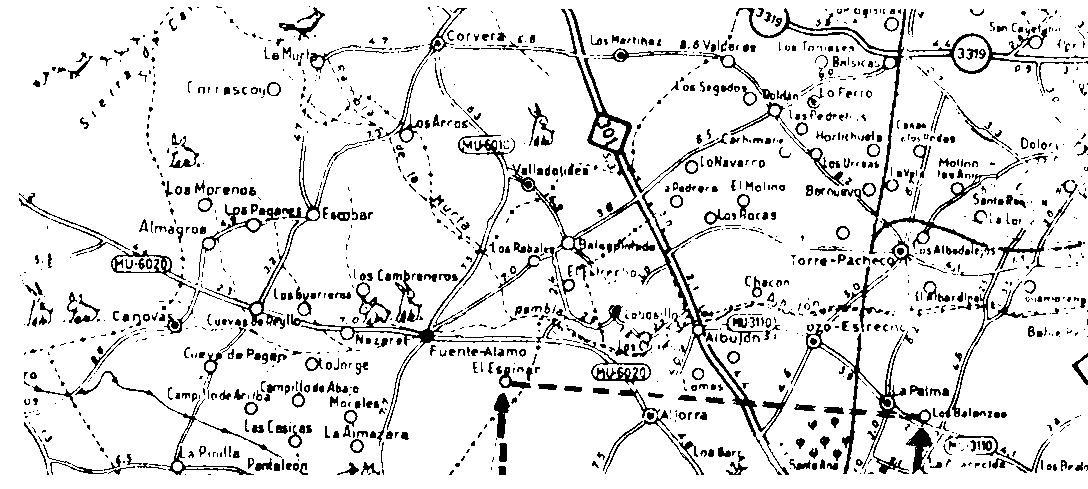
Este trozo que sobra (a-b) lo llevamos a la "contraescala", a partir del cero hacia la izquierda, en donde vemos que corresponde a 1 Km. mas otro trocito, que por aproximación y "a ojo" deben ser 0.7 km
Por lo tanto, la distancia entre ambos pueblos es de:
15 + 1 + 0.7 = 16.7 km
| Orientación |
Es la forma de relacionar la posición del mapa con respecto a los "puntos cardinales", tal y como es en la realidad el terreno en relación a tales "puntos cardinales".
En los mapas, cartas o planos a veces se señala la orientación por medio de la "rosa de los vientos", aunque es suficiente y lo más frecuente, señalar simplemente la dirección Norte bien mediante una flecha con la letra N, o bien con cualquier indicativo o alegoría que indique tal dirección.
Si no llevan ninguna indicación de orientación, se sobrentiende que esta orientado al Norte en la posición normal de lectura del plano.
| Signos convencionales |
Generalmente es fácil la comprensión de los símbolos o abreviaturas empleadas en los planos, los cuales conocemos, por la costumbre de haber interpretado diversos planos a lo largo de nuestra vida.
Así, por ejemplo, una carretera se representa mediante dos líneas paralelas, (y si es en colores, generalmente de color rojo). Un río se dibuja mediante una o mas líneas temblorosas, (que no es ni más ni menos que la forma que tiene el río en la realidad), siendo de color azul cuando el plano es en colores.
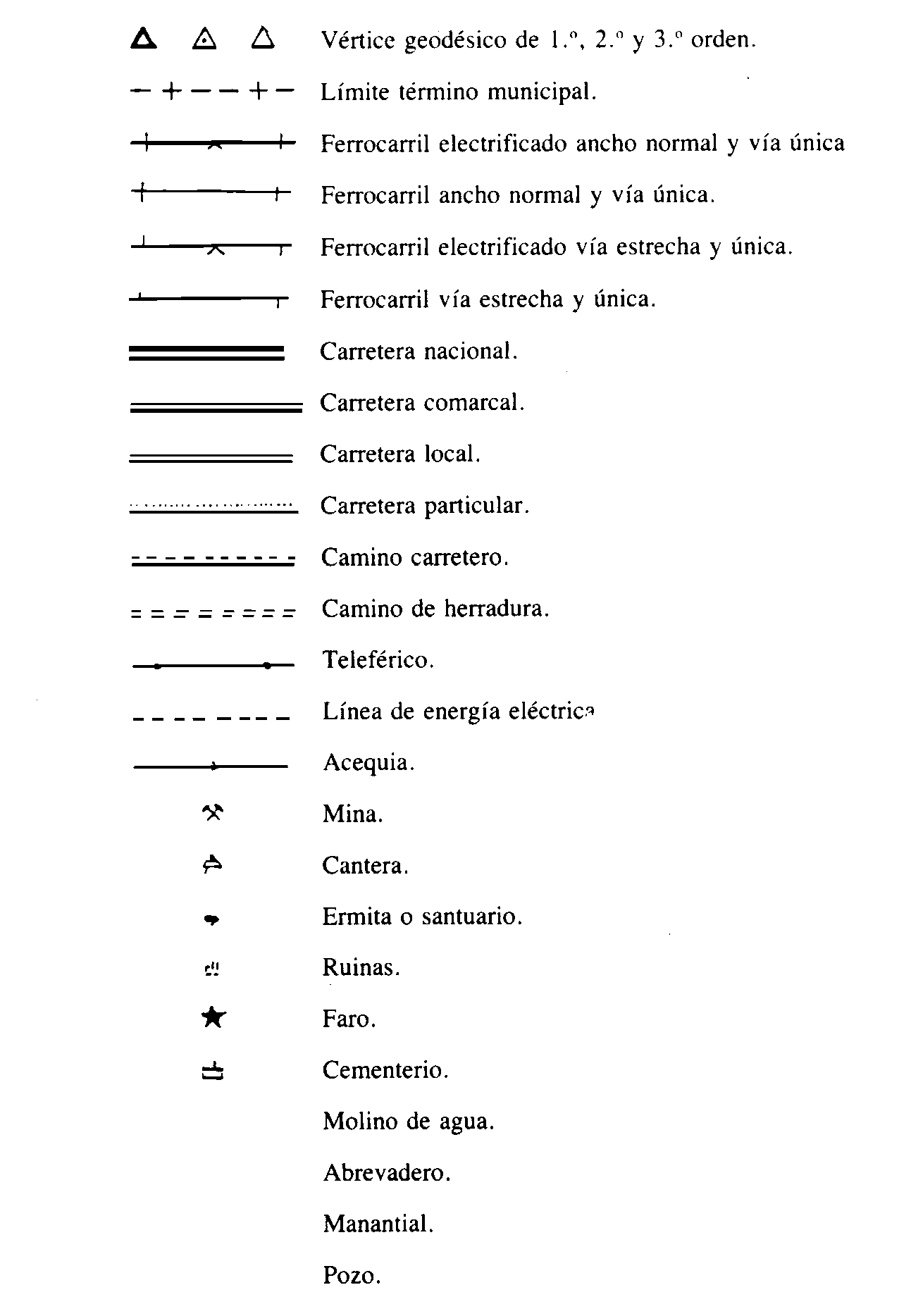
Signos convencionales en un "Plano turístico"

Del mismo modo se emplean símbolos o abreviaturas, que indican determinados accidentes o puntos notorios, bien cultivos o curvas de nivel, etc.
No obstante casi todos los planos, mapas y cartas llevan aparte, unos dibujos o símbolos, bajo el nombre de "Símbolos convencionales" o bien "Leyenda", en donde se explica lo que significa cada uno e incluso la importancia o notoriedad del mismo.
| Curvas de nivel |
Es el procedimiento que se emplea para poder dibujar y saber interpretar, con cierta exactitud, el relieve del terreno.
Existen otros procedimientos para dar idea del relieve, tales como el sombreado con diversos colores, o bien dibujando pequeños montes agrupados o no según la importancia del relieve.
Pero el método mas exacto, preciso y fácil de manejar para determinados cálculos es el procedimiento de "curvas de nivel".
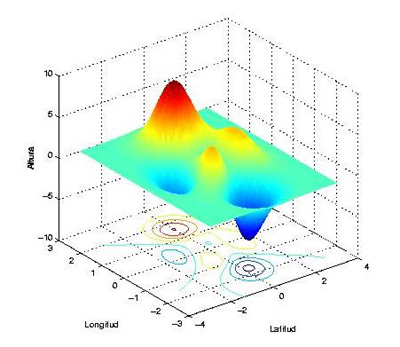
Se define curva de nivel como la línea imaginaria o real, que une todos los puntos del terreno o del plano que tienen la misma cota.
El ejemplo mas claro de lo que es una curva de nivel, nos lo da una orilla de un lago o pantano cuando la superficie del agua esta totalmente quieta.
Las curvas de nivel de los terrenos de poca superficie, en los que se puede prescindir de la esfericidad terrestre, vendrán dados por la proyección sobre el "plano de comparación" de las intersecciones de la superficie con planos paralelos, a la misma distancia unos de otros, es decir, equidistantes. De aquí que se llame quot;equidistancia" a la distancia que existe entre dos planos inmediatos.
Al igual que ocurre con las escalas, la equidistancia puede ser cualquier cantidad, y siempre se toman valores de ella en función de la escala del plano, de la finalidad del mapa y de las consecuencias o estudios a obtener de el.
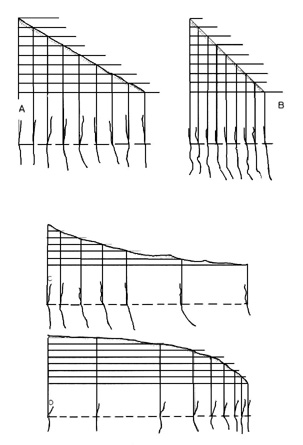
Las curvas de nivel separadas a distancias muy regulares indican que la pendiente es uniforme.
Si las curvas están muy separadas en una determinada dirección indican una pendiente suave (figura A).
Si las curvas están más próximas, la pendiente seguirá siendo uniforme, pero será más escarpada (figura B). Si se trata de una colina donde la línea que pretendemos seguir muestra que las curvas de nivel en la parte superior están más próximas entre sí que las de la parte inferior, sabremos que la pendiente se hace más escarpada al acercarse a la cumbre (figura C).
Si las líneas están más próximas hacia el nivel inferior, la colina será más plana en la cumbre y la pendiente será mas escarpada hacia su base (figura D).
| Características de las curvas de nivel |
Por lo visto anteriormente, podemos sacar unas cuantas conclusiones de las curvas de nivel, las cuales hay que tener en cuenta, a la hora de tratar de representar en un plano un terreno determinado o bien de interpretar el terreno a partir de un mapa o plano:
- Toda curva de nivel es cerrada. En todo mapa o plano estará cerrada bien dentro o bien fuera de él.
- Dos curvas no pueden cortarse.
- Dos o mas curvas pueden unirse o confundirse en una sola en un punto o en un tramo (pendientes de 90 grados).
- Una curva de nivel no puede dividirse en dos o mas curvas.
| Otro sistema de representación del relieve. Planos acotados |
Es un sistema muy usado en Taquimetría. En este sistema todo punto del espacio le corresponde uno y solamente uno, en un plano, que hemos tomado arbitrariamente y que llamamos "plano de comparación".
Así al punto A del espacio, le corresponde el "a" en el plano de comparación, habiendo obtenido el "a" por la intersección de la perpendicular de A al plano, con este.
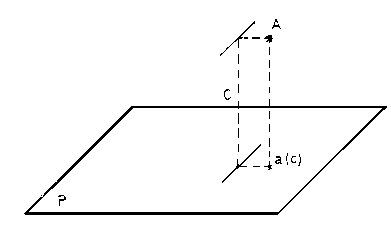
Ahora bien, todo sistema de representación tiene que ser reversible, es decir, que con la contemplación del plano P debemos saber que lugar ocupa el punto "A" en el espacio. Si no añadiésemos nada mas de lo dicho hasta ahora, lo único que sabríamos sería que el punto "A" se encuentra en uno de los infinitos puntos de la recta "A-a".Este dato que precisamos para conocer donde se encuentra el punto "A", es la distancia que le separa del plano, en nuestro caso "C". A este dato se le llama "cota".
Cota, es la altura de un punto del terreno con respecto al nivel del mar, o bien con respecto al plano de comparación.
La cota de un punto del terreno se señala en su homólogo del plano, colocando junto a el, la cifra que la expresa encerrada en un paréntesis, y generalmente expresada en metros.
La cota puede ser positiva, negativa o nula, según que el punto "A" se encuentre por encima, por debajo, a nivel del mar o del plano de comparación.
De todo lo anterior se deduce que una recta "A-B" del terreno queda representada en el plano de comparación, por la proyección de sus extremos "a" y "b", (ver figura).
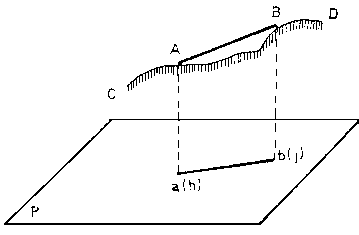
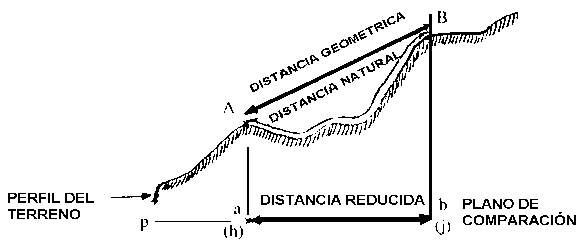
Si la línea sinuosa "C-D" es la del perfil del terreno y a ella pertenecen los puntos "A" y "B", podemos deducir los siguientes conceptos:
- La distancia entre "A" y "B", siguiendo las sinuosidades del terreno, es decir midiendo con cinta dejándola totalmente floja y adaptada al relieve, se denomina "distancia natural".
- La distancia de la recta "A-B", medida tensando lo mas posible la cinta métrica, se la denomina "distancia geométrica".
- La distancia entre los puntos "a" y "b", que es la que figura en los planos y que es la resultante de proyectar los puntos "A" y "B" del terreno, se denomina "distancia reducida" y se obtiene en campo tensando la cinta métrica lo más posible y colocándola horizontalmente.
Se llama "desnivel", a la diferencia entre las cotas de los puntos "A" y "B", es decir, (j) - (h).
Otro término muy usado en topografía y que sirve para otros muchos cálculos es el de "pendiente".
| Pendientes |
Es el cociente entre el "desnivel" y la "distancia reducida", expresada en tanto por ciento (%).
Viene dada por la siguiente fórmula:
P = (Z/d) * 100 = {[(j) - (h)] / d } * 100
En donde:
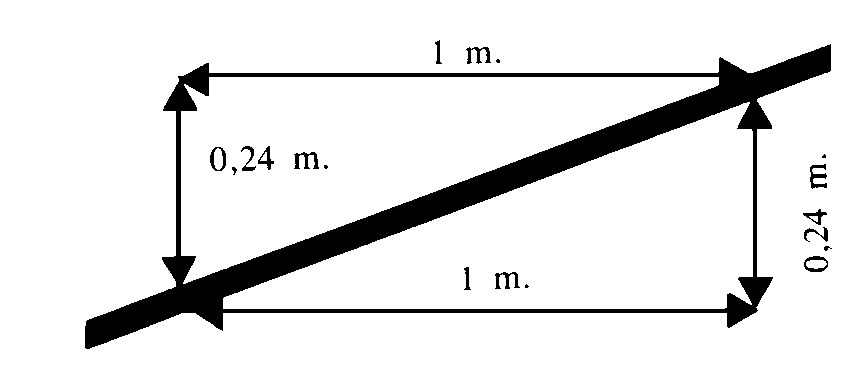
P = ( 24 / 100 ) * 100 = 24%
Otra forma de expresar la pendiente es mediante grados de inclinación, con respecto a la horizontal.
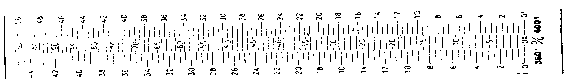
El gráfico relaciona las pendientes, expresadas en % con sus pendientes equivalentes, expresadas en grados sexagesimales y centesimales. Las pendiente obtenidas en % se convierten en grados de pendiente así:
Ejemplos: 12% = 6º 50' = 7g. 60 m.
28% = 15º 40' = 17g. 40 m.
70% = 35º -- = 38g. 90 m.
| Laderas y cuestas |
Es la forma más sencilla de interpretar las curvas de nivel. Estas se aproximan a líneas rectas paralelas entre sí.
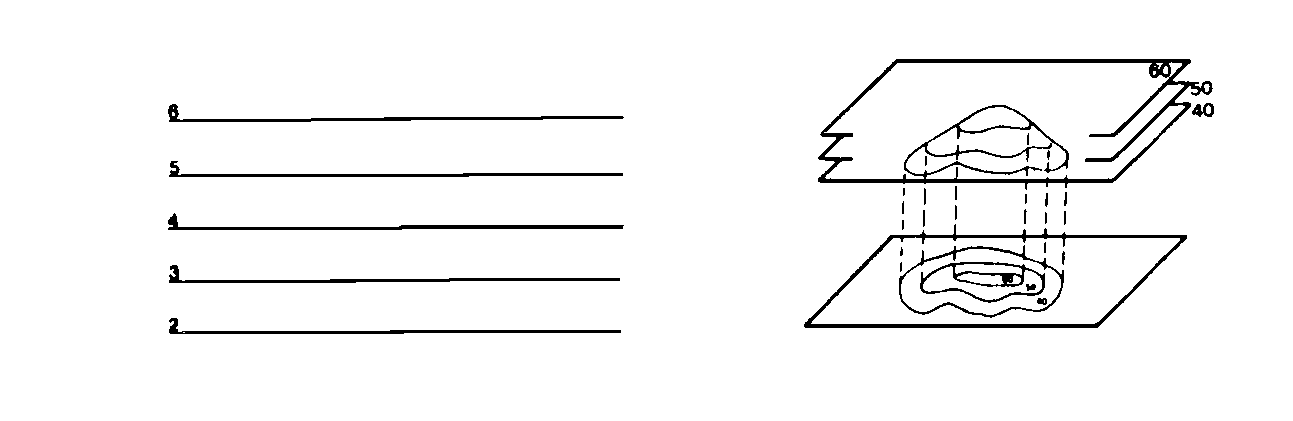
Llamamos "línea de máxima pendiente", en una ladera, a la perpendicular a las curvas de nivel, y se denomina "pendiente de una ladera", a la inclinación respecto a la horizontal de su línea de máxima pendiente. De dos laderas representadas por curvas de nivel de igual equidistancia, es más pendiente aquella cuyas curvas de nivel presentan menor distancia entre si.
| Perfiles |
Muchas veces para darse una idea exacta de la forma del terreno, se recurre a la obtención de "perfiles".
Un "perfil" es la intersección de un plano vertical con los horizontales, (que son los que nos dan las curvas de nivel) y, después se hace girar el plano vertical hasta que coincida con el de comparación.
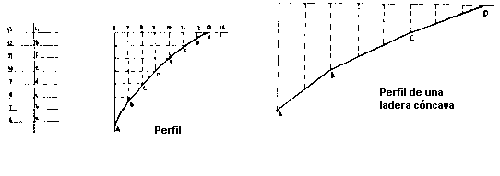
Una ladera no tiene por que ser de igual pendiente en todo su descenso o ascenso. En todo caso estará formada por dos o mas laderas. Viendo la figura, en la que se representa el perfil de una ladera, se comprende lo que queremos decir.
La ladera esta formada por tres cuestas con diferentes pendientes. El tramo A-B es el de mayor pendiente, le sigue después el B-C y, por último, el C-D. En este caso las tres cuestas se unen entre si por líneas horizontales y paralelas a las curvas de nivel, pues bien, a estas intersecciones se les llaman "líneas de cambio de pendiente". Hay que aclarar también que las líneas de cambio de pendiente no tienen que ser forzosamente horizontales.
Las laderas, con arreglo a su perfil, se pueden dividir en "cóncavas"y "convexas".
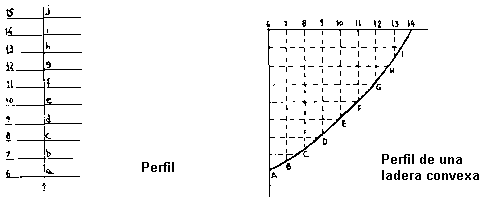
Cuando en un plano nos encontramos curvas de nivel sensiblemente rectas y paralelas entre si, tal que la distancia en la proyección disminuye en el sentido ascendente de las curvas de nivel, se trata de una ladera "cóncava". Al contrario, cuando la distancia de las curvas de nivel en la proyección se va haciendo mayor, en el sentido ascendente del terreno, tendremos una ladera "convexa".
| Entrantes y salientes |
Veamos que sucede cuando dos laderas se unen y su intersección deja de ser horizontal.
Supongamos dos casos: que las líneas de menor cota envuelvan a las de mayor y, al contrario, que las de mayor cota envuelvan a las de menor.
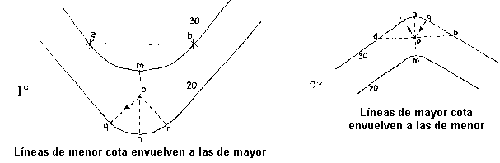
En el primer caso, si unimos dos puntos de una misma curva de nivel, en nuestro caso "a" y "b", uno de cada ladera, la recta "a-b" atraviesa el terreno y se dice entonces que la intersección "m-n" forma un "saliente", de tal forma que el agua que caiga en un punto "P" de la intersección seguirá dos caminos: "P-q" y "P-r", que son las líneas de máxima pendiente; luego el agua se dividirá, cayendo por cada ladera, las cuales reciben el nombre de "vertientes". A la línea que une las dos laderas se le llama "divisoria".
En el segundo caso, si unimos dos puntos de una misma curva de nivel, uno de cada ladera, en nuestro caso "a" y "b", la recta "a-b" es exterior al terreno y la intersección forma un "entrante". Al igual que en el caso anterior, el agua que caiga, por ejemplo, en "q" y "r", seguirá la línea de máxima pendiente hasta encontrarse en la intersección "m-n", y bajara por ella. En este caso, a esta línea se le llama "vaguada".
| Cerros, valles y puertos |
Cuando las curvas de menos cota envuelven a las de mayor cota, se dice que el terreno forma una elevación, que según su importancia se le llamará "pico", "cerro", "colina", "montaña", etc.
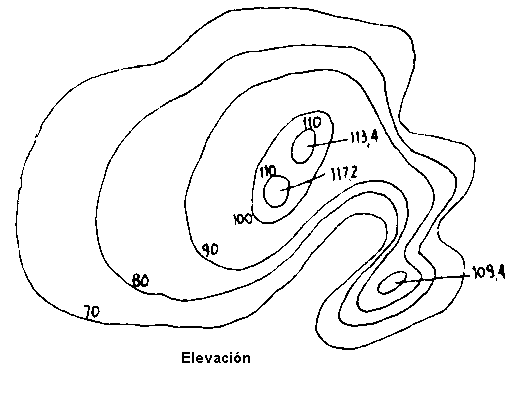
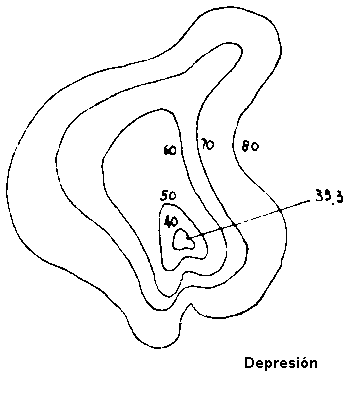
Por el contrario, cuando sean las de mayor cota las que envuelven a las de menor, se trata de una "depresión", que si es de gran amplitud le llamamos "valle".
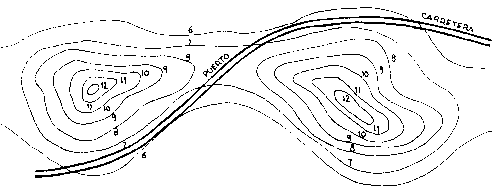
Se llama "puerto" a un paso estrecho entre montañas; pues bien en un mapa con curvas de nivel vendrá dado, mas o menos como se indica en la figura siguiente.
| Medidas angulares |
Los ángulos horizontales se miden en topografía de izquierda a derecha, o sea, siguiendo el sentido de las agujas del reloj. Pero tenemos tres unidades para medir estos ángulos, que serán:
Grados sexagesimales |
Resultan de dividir la circunferencia en 360 partes iguales, a las que llamaremos grados; cada grado en 60 minutos, y cada minuto en 60 segundos. |
Grados centesimales |
Resultan
de dividir la circunferencia en 400 partes iguales, llamadas también grados, cada grado en 100 minutos, y cada minuto en 100 segundos. |
Milésima o milésima militar |
Resulta
de dividir la circunferencia en 6.400 partes iguales cada una de ellas es una milésima militar, sin confundirla con la milésima geométrica, un poco mayor que esta. |
| Distancias que se consideran en el terreno y en el plano |
- Distancia real o topográfica: es la distancia verdadera del terreno que separa dos puntos.
- Distancia natural o geométrica: es la distancia en línea recta que separa dos puntos del terreno.
- Distancia horizontal, reducida o reducida al horizonte: se llama de estas tres formas a la longitud de la recta perpendicular, a las verticales que pasan por los extremos de la distancia.
- Diferencia de nivel: es la distancia vertical que separa dos puntos del terreno. Se halla restando la cota menor de un punto, de la mayor de otro.
En el plano encontraremos siempre distancias reducidas; para deducir la distancia natural, conociendo la distancia reducida y la diferencia de nivel, tendremos que hacer una construcción geográfica o seguir un procedimiento aritmético (teorema de Pitágoras).
| Coordenadas geográficas |
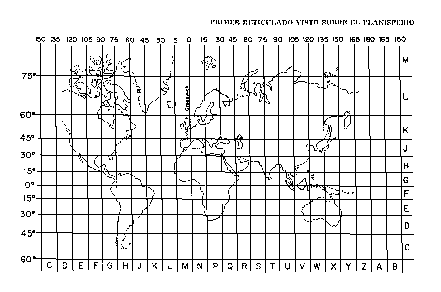
Si trazamos en torno de la tierra una serie de anillos paralelos al ecuador y luego una segunda serie, esta vez de anillos perpendiculares al ecuador y convergentes en ambos polos, tendremos una red de líneas de referencia que nos servirán para localizar con exactitud cualquier punto de la superficie terrestre.
La distancia que media entre un punto determinado y el ecuador se llama latitud. Esta será "Norte" o "Sur" según que el punto esté situado al Norte o al Sur del ecuador. Los anillos que corren paralelamente al ecuador reciben el nombre de "paralelos de latitud" o, simplemente, paralelos.
A los aún poco versados en la lectura de mapas les extraña el hecho de que, corriendo los paralelos de Este a Oeste, las distancias Norte-Sur se midan entre ellos. Los anillos de la segunda serie, que forman ángulo recto con los paralelos y pasan por los polos, se conocen por el nombre de "meridianos de longitud" o, mas sencillamente, meridianos. Estos van de Norte a Sur, pero las distancias Este-Oeste se miden entre un meridiano y otro. Se dirá, pues, longitud "Este" u "Oeste" respecto del primer meridiano.
Las coordenadas geográficas se expresan en medidas angulares. Cada círculo esta dividido en 360 grados, cada grado en 60 minutos y cada minuto en 60 segundos. A partir de 0º en el ecuador, los paralelos de latitud van numerándose hasta 90º, tanto hacia el Norte como hacia el Sur. Los extremos son el Polo Norte, a 90º de "latitud Norte", y el Polo Sur, a 90º de "latitud Sur".
Como la latitud puede tener el mismo valor numérico al Norte o al Sur del ecuador, ha de indicarse siempre la dirección (N o S). Comenzando de 0º en el primer meridiano, la longitud se mide al Este o al Oeste. Las líneas situadas al Este del primer meridiano se expresan en grados (hasta 180º) de "longitud Este". También aquí debe siempre mencionarse la dirección (E u O). La longitud de la línea opuesta (180º) al primer meridiano se llama indiferentemente "Este" u "Oeste". Por ejemplo, resumiendo lo que acabamos de ver, la "x" en la figura representa un punto situado a 58º de latitud Norte y 80º de longitud Este. En forma escrita, la latitud de indica siempre en primer lugar. Sus coordenadas geográficas se expresaran por lo tanto de la siguiente manera: 58ºN 80ºE.

Los valores de las coordenadas geográficas, formulados en unidades de medición angular, tendrán mas sentido para nosotros si comparamos dichas unidades con otras que nos resulten mas familiares. Así, en cualquier punto de la Tierra, la distancia lineal equivalente a 1º de longitud es de unos 111 km; 1 segundo equivale poco mas o menos a 30 m.
La distancia correspondiente a 1º de latitud en el ecuador es también de unos 111 km, pero disminuye a medida que nos movemos hacia el Norte o el Sur, hasta llegar a cero en los polos.
Como ya hemos dicho, los mapas publicados en algunos países no basan sus longitudes en el mismo "primer meridiano" que nosotros, es decir, el de Greenwich. Cuando tales mapas se venden o distribuyen en España, la información marginal contiene de ordinario una nota indicando la diferencia existente entre el meridiano de Greenwich y el primer meridiano del mapa en cuestión. Para convertir las longitudes de ese mapa en las de Greenwich, deben añadirse o substraerse (según que el punto escogido se encuentre al Este o al Oeste del meridiano de Greenwich).
En España nos podremos encontrar algunos planos con referencia al meridiano de Madrid, por lo que la diferencia será de 3º 41' 15" W (Oeste).

| Identificación de la longitud y la latitud |
Si se desea averiguar la latitud y la longitud de un lugar determinado, tendrá que descubrir lo que ya está señalado en el mapa y avanzar partiendo de ello. Si se trata de un mapa a gran escala, probablemente encontrará coordenadas a lo largo del margen señaladas en grados y minutos.
En la mayoría de las escalas, las graduaciones no serán menores que los 30' (medio grado). Si las líneas no atraviesan el mapa, trace líneas rectas con un lápiz uniendo las marcas que se encuentran a los lados del mapa. (figura A).

Trace líneas paralelas a éstas atravesando el punto que desea identificar (figura B). La latitud y longitud del punto se determinarán por la proporción. Si la diferencia entre dos señales conocidas es de 5', deberá medir a qué proporción de la distancia se encuentra la línea que ha trazado y traducirlo en minutos. Suponga que la distancia en milímetros es de 100 al Oeste del punto de longitud más cercano, y la distancia entre las señales es de 300 milímetros. A partir de los datos indicados en las marcas, usted podrá observar que la diferencia es de 5'. Para averiguar a qué distancia hacia el Oeste se encuentra el lugar, calcule proporcionalmente:
100 / 300 * 5 = 1.66 minutos
Para traducirlo en minutos y segundos, multiplique la parte decimal por 60, con lo cual obtendrá 40, por lo tanto la cifra será de 1'40''. A ello debe añadirse la lectura más próxima del Este a fin de obtener la longitud del punto. En este caso, son 7º 30', de modo que la longitud del lugar es de 7º 31' 40''. Es posible que el mapa incluya tan sólo los grados en las esquinas del mapa, mientras que los puntos intermedios se señalan en minutos y segundos.
La latitud se determina del mismo modo, pero esta vez en dirección Norte (figura D). Mida la distancia desde el punto señalado más cercano al punto que se quiere determinar la latitud, averigüé la distancia entre los puntos señalados y efectúe el cálculo proporcional a fin de obtener los minutos y segundos que se añadirán a la lectura más próxima en dirección Sur (figura E).
| Coordenadas de las Capitales de Provincia. (por el meridiano de Greenwich) |
| Capital | Latitud N. | Longitud |
|---|---|---|
| Albacete | 38º 59' 44.1" | 01º 51' 21" W |
| Alicante / Alacant | 38º 20' 54.3" | 00º 28' 47" W |
| Almeria | 36º 49' 36.0" | 02º 27' 56" W |
| Avila | 40º 39' 20.6" | 04º 41' 51" W |
| Badajoz | 38º 52' 55.2" | 06º 58' 03" W |
| Barcelona | 41º 23' 02.5" | 02º 10' 36" E |
| Bilbao | 43º 15' 26.0" | 02º 55' 26" W |
| Burgos | 42º 20' 25.3" | 03º 42' 16" W |
| Cáceres | 39º 28' 22.8" | 06º 22' 15" W |
| Cádiz | 36º 31' 54.7" | 06º 17' 52" W |
| Castellón | 39º 59' 10.0" | 00º 12' 15" W |
| Ceuta | 35º 53' | 05º 18' W |
| Ciudad Real | 38º 59' 11.7" | 03º 55' 52" W |
| Córdoba | 37º 52' 46.1" | 04º 46' 48" W |
| Coruña, A | 43º 22' 12.5" | 08º 23' 27" W |
| Cuenca | 40º 04' 35.1" | 02º 07' 54" W |
| Girona | 41º 58' 55.1" | 02º 49' 27" E |
| Granada | 37º 10' 34.9" | 03º 36' 00" W |
| Guadalajara | 40º 38' 04.1" | 03º 09' 45" W |
| Huelva | 37º 15' 35.9" | 06º 57' 00" W |
| Huesca | 42º 08' 25.8" | 00º 24' 32" W |
| Jaén | 37º 45' 54.4" | 03º 47' 24" W |
| León | 42º 35' 56.9" | 05º 34' 01" W |
| Lleida | 41º 37' 02.5" | 00º 37' 36" E |
| Logroño | 42º 27' 59.2" | 02º 26' 45" W |
| Lugo | 43º 00' 33.7" | 07º 33' 28" W |
| Madrid | 40º 24' 30.0" | 03º 41' 15" W |
| Málaga | 36º 43' 12.9" | 04º 24' 50" W |
| Melilla | 35º 27' | 02º 33' W |
| Murcia | 37º 59' 03.5" | 01º 07' 42" W |
| Ourense | 42º 20' 11.2" | 07º 51' 48" W |
| Oviedo | 43º 21' 44.2" | 05º 50' 36" W |
| Palencia | 42º 00' 27.8" | 04º 32' 04" W |
| Palma de Mallorca | 39º 34' 31.5" | 02º 39' 07" E |
| Palmas, Las | 28º 05' 57.8" | 15º 24' 48" W |
| Pamplona | 42º 49' 10.9" | 01º 38' 30" W |
| Pontevedra | 42º 26' 01.4" | 08º 38' 51" W |
| Salamanca | 40º 57' 39.5" | 05º 40' 00" W |
| San Sebastian / Donostia | 43º 19' 01.3" | 01º 58' 54" W |
| Santa Cruz de Tenerife | 28º 27' 22.8" | 16º 14' 02" W |
| Santander | 43º 27' 47.7" | 03º 48' 19" W |
| Segovia | 40º 57' 00.4" | 04º 07' 33" W |
| Sevilla | 37º 23' 10.0" | 05º 59' 33" W |
| Soria | 41º 46' 06.3" | 02º 28' 00" W |
| Tarragona | 41º 15' 12.3" | 01º 22' 13" E |
| Teruel | 40º 20' 38.7" | 01º 06' 33" W |
| Toledo | 39º 51' 25.6" | 04º 01' 27" W |
| Valencia | 39º 28' 30.7" | 00º 22' 33" W |
| Valladolid | 41º 39' 08.0" | 04º 43' 24" W |
| Vitoria / Gasteiz | 42º 50' 50.8" | 02º 40' 18" W |
| Zamora | 41º 29' 56.1" | 05º 45' 16" W |
| Zaragoza | 41º 39' 24.2" | 00º 52' 47" W |
| Coordenadas de las de las principales ciudades de España |
| Provincia | Ciudad | Latitud | Longitud |
|---|---|---|---|
| Alava | Amurrio | 43.03 N | 3.00 O |
| Alava | Laguardia | 42.33 N | 2.35 O |
| Alava | Vitoria | 42.51 N | 2.41 O |
| Albacete | Albacete | 39.00 N | 1.52 O |
| Albacete | Alcaraz | 38.40 N | 2.29 O |
| Albacete | Almansa | 38.52 N | 1.06 O |
| Albacete | Casas Ibañez | 39.17 N | 1.29 O |
| Albacete | Chinchilla | 38.55 N | 1.43 O |
| Albacete | Hellin | 38.31 N | 1.42 O |
| Albacete | Munera | 39.02 N | 2.29 O |
| Albacete | Villarrobledo | 39.16 N | 2.36 O |
| Albacete | Yeste | 38.22 N | 2.19 O |
| Alicante | Alcoy | 38.42 N | 0.28 O |
| Alicante | Alicante | 38.20 N | 0.29 O |
| Alicante | Altea | 38.36 N | 0.03 O |
| Alicante | Benidorm | 38.32 N | 0.08 O |
| Alicante | Callosa d'En Sarria | 38.40 N | 0.08 O |
| Alicante | Callosa de Segura | 38.01 N | 0.53 O |
| Alicante | Cocentaina | 38.45 N | 0.26 O |
| Alicante | Denia | 38.50 N | 0.07 O |
| Alicante | Elda | 38.29 N | 0.47 O |
| Alicante | Elche | 38.15 N | 0.42 O |
| Alicante | Jijona | 38.32 N | 0.30 O |
| Alicante | Monovar | 38.26 N | 0.51 O |
| Alicante | Novelda | 38.23 N | 0.45 O |
| Alicante | Orihuela | 38.05 N | 0.57 O |
| Alicante | Pego | 38.51 N | 0.08 O |
| Alicante | Torrevieja | 37.59 N | 0.40 O |
| Alicante | Villajoyosa | 38.30 N | 0.14 O |
| Alicante | Villena | 38.39 N | 0.52 O |
| Almeria | Adra | 36.45 N | 3.00 O |
| Almeria | Almeria | 36.50 N | 2.28 O |
| Almeria | Berja | 36.51 N | 2.56 O |
| Almeria | Canjayar | 37.01 N | 2.44 O |
| Almeria | Huercal Overa | 37.23 N | 1.57 O |
| Almeria | Nijar | 36.58 N | 2.12 O |
| Almeria | Purchena | 37.21 N | 2.21 O |
| Almeria | Roquetas de Mar | 36.46 N | 2.37 O |
| Almeria | Sorbas | 37.06 N | 2.08 O |
| Almeria | Velez Rubio | 37.39 N | 2.05 O |
| Almeria | Vera | 37.15 N | 1.53 O |
| Andorra | Andorra la Vella | 42.30 N | 1.28 E |
| Asturias | Aller | 43.10 N | 5.38 O |
| Asturias | Aviles | 43.33 N | 5.56 O |
| Asturias | Belmonte-Miranda | 43.17 N | 6.12 O |
| Asturias | Cangas de Narcea | 43.10 N | 6.32 O |
| Asturias | Cangas de Onis | 43.21 N | 5.08 O |
| Asturias | Castropol | 43.32 N | 7.00 O |
| Asturias | Gijon | 43.32 N | 5.42 O |
| Asturias | Grado | 43.23 N | 6.07 O |
| Asturias | Infiesto | 43.21 N | 5.21 O |
| Asturias | Langreo | 43.18 N | 5.41 O |
| Asturias | Luarca | 43.32 N | 6.32 O |
| Asturias | Llanes | 43.25 N | 4.45 O |
| Asturias | Mieres | 43.15 N | 5.46 O |
| Asturias | Navia | 43.33 N | 6.42 O |
| Asturias | Oviedo | 43.22 N | 5.50 O |
| Asturias | Pola de Lena | 43.10 N | 5.49 O |
| Asturias | Pola de Siero | 43.24 N | 5.39 O |
| Asturias | Pravia | 43.30 N | 6.07 O |
| Asturias | Ribadesella | 43.28 N | 5.07 O |
| Asturias | Tineo | 43.20 N | 6.25 O |
| Asturias | Villaviciosa | 43.28 N | 5.27 O |
| Avila | Arenas de San Pedro | 40.12 N | 5.05 O |
| Avila | Arevalo | 41.04 N | 4.43 O |
| Avila | Avila | 40.39 N | 4.42 O |
| Avila | El Barco de Avila | 40.21 N | 5.31 O |
| Avila | Cebreros | 40.27 N | 4.28 O |
| Avila | Piedrahita | 40.28 N | 5.20 O |
| Badajoz | Alburquerque | 39.13 N | 6.59 O |
| Badajoz | Almendralejo | 38.41 N | 6.24 O |
| Badajoz | Azuaga | 38.16 N | 5.41 O |
| Badajoz | Badajoz | 38.53 N | 6.58 O |
| Badajoz | Cabeza del Buey | 38.43 N | 5.13 O |
| Badajoz | Castuera | 38.43 N | 5.32 O |
| Badajoz | Don Benito | 38.57 N | 5.52 O |
| Badajoz | Fregenal de la Sierra | 38.10 N | 6.39 O |
| Badajoz | Fuente de Cantos | 38.14 N | 6.18 O |
| Badajoz | Herrera del Duque | 39.10 N | 5.03 O |
| Badajoz | Jerez de los Caballeros | 38.20 N | 6.46 O |
| Badajoz | Llerena | 38.14 N | 6.01 O |
| Badajoz | Merida | 38.55 N | 6.20 O |
| Badajoz | Montijo | 38.54 N | 6.37 O |
| Badajoz | Olivenza | 38.41 N | 7.06 O |
| Badajoz | Puebla de Alcocer | 38.59 N | 5.15 O |
| Badajoz | Villanueva de la Serena | 38.59 N | 5.48 O |
| Badajoz | Villanueva del Fresno | 38.23 N | 7.10 O |
| Badajoz | Zafra | 38.26 N | 6.25 O |
| Ibiza | Ibiza | 38.54 N | 1.26 E |
| Ibiza | San Antonio | 38.59 N | 1.19 E |
| Ibiza | San Juan | 39.05 N | 1.31 E |
| Mallorca | Alcudia | 39.51 N | 3.23 E |
| Mallorca | Andraitx | 39.35 N | 2.25 E |
| Mallorca | Arta | 39.42 N | 3.21 E |
| Mallorca | Felanitx | 39.28 N | 3.10 E |
| Mallorca | Inca | 39.43 N | 2.55 E |
| Mallorca | Lluchmajor | 39.29 N | 2.53 E |
| Mallorca | Manacor | 38.34 N | 3.13 E |
| Mallorca | Palma de Mallorca | 39.35 N | 2.39 E |
| Mallorca | Soller | 39.46 N | 2.43 E |
| Menorca | Ciudadela | 40.00 N | 3.50 E |
| Menorca | Mahon | 39.53 N | 4.16 E |
| Barcelona | Arenys de Mar | 41.35 N | 2.33 E |
| Barcelona | Badalona | 41.27 N | 2.15 E |
| Barcelona | Barcelona | 41.23 N | 2.11 E |
| Barcelona | Berga | 42.06 N | 1.51 E |
| Barcelona | Calella | 41.37 N | 2.40 E |
| Barcelona | Cardona | 41.56 N | 1.49 E |
| Barcelona | Cerdanyola del Valles | 41.30 N | 2.09 E |
| Barcelona | Esparraguera | 41.33 N | 1.52 E |
| Barcelona | Gava | 41.18 N | 2.00 E |
| Barcelona | Gironella | 42.02 N | 1.53 E |
| Barcelona | Granollers | 41.37 N | 2.18 E |
| Barcelona | Hospitalet de Llobregat | 41.22 N | 2.08 E |
| Barcelona | Igualada | 41.35 N | 1.37 E |
| Barcelona | Malgrat | 41.39 N | 2.45 E |
| Barcelona | Manlleu | 42.00 N | 2.17 E |
| Barcelona | Manresa | 41.43 N | 1.50 E |
| Barcelona | Martorell | 41.28 N | 1.56 E |
| Barcelona | Mataro | 41.32 N | 2.27 E |
| Barcelona | Mollet del Valles | 41.33 N | 2.13 E |
| Barcelona | El Prat de Llobregat | 41.18 N | 2.03 E |
| Barcelona | Sabadell | 41.33 N | 2.07 E |
| Barcelona | Sallent | 41.50 N | 1.54 E |
| Barcelona | Sant Boi de Llobregat | 41.20 N | 2.03 E |
| Barcelona | Sant Celoni | 41.42 N | 2.30 E |
| Barcelona | Sant Feliu de Llobregat | 41.23 N | 2.03 E |
| Barcelona | Sant Sadurni d'Anoia | 41.26 N | 1.47 E |
| Barcelona | Santa Coloma de Gramanet | 41.27 N | 2.13 E |
| Barcelona | Sitges | 41.14 N | 1.48 E |
| Barcelona | Terrassa | 41.34 N | 2.01 E |
| Barcelona | Vic | 41.56 N | 2.15 E |
| Barcelona | Vilafranca del Penedes | 41.22 N | 1.41 E |
| Barcelona | Vilanova i la Geltru | 41.13 N | 1.43 E |
| Burgos | Aranda de Duero | 41.39 N | 3.42 O |
| Burgos | Belorado | 42.26 N | 3.12 O |
| Burgos | Briviesca | 42.33 N | 3.19 O |
| Burgos | Burgos | 42.20 N | 3.42 O |
| Burgos | Castrojeriz | 42.17 N | 4.09 O |
| Burgos | Lerma | 42.02 N | 3.45 O |
| Burgos | Miranda de Ebro | 42.41 N | 2.56 O |
| Burgos | Salas de los Infantes | 42.03 N | 3.16 O |
| Burgos | Sedano | 42.43 N | 3.45 O |
| Burgos | Villadiego | 42.31 N | 4.01 O |
| Burgos | Villarcayo | 42.56 N | 3.34 O |
| Caceres | Alcantara | 39.43 N | 6.53 O |
| Caceres | Caceres | 39.28 N | 6.22 O |
| Caceres | Coria | 39.59 N | 6.33 O |
| Caceres | Garrovillas | 39.43 N | 6.33 O |
| Caceres | Hervas | 40.16 N | 5.52 O |
| Caceres | Hoyos | 40.11 N | 6.43 O |
| Cáceres | Jarandilla de la Vera | 40.08 N | 5.39 O |
| Cáceres | Logrosan | 39.20 N | 5.30 O |
| Cáceres | Montanchez | 39.14 N | 6.09 O |
| Cáceres | Navalmoral de la Mata | 39.53 N | 5.33 O |
| Cáceres | Plasencia | 40.02 N | 6.06 O |
| Cáceres | Trujillo | 39.28 N | 5.53 O |
| Cáceres | Valencia de Alcantara | 39.25 N | 7.14 O |
| Cáceres | Zorita | 39.17 N | 5.42 O |
| Cádiz | Alcala de los Gazules | 36.28 N | 5.43 O |
| Cádiz | Algeciras | 36.11 N | 5.27 O |
| Cádiz | Arcos de la Frontera | 36.45 N | 5.49 O |
| Cádiz | Cadiz | 36.32 N | 6.18 O |
| Cádiz | Chiclana de la Frontera | 36.25 N | 6.09 O |
| Cádiz | Grazalema | 36.46 N | 5.22 O |
| Cádiz | Jerez de la Frontera | 36.41 N | 6.09 O |
| Cádiz | Medina Sidonia | 36.28 N | 5.56 O |
| Cádiz | Olvera | 36.56 N | 5.16 O |
| Cádiz | Puerto de Santa Maria | 36.36 N | 6.13 O |
| Cádiz | San Fernando | 36.28 N | 6.11 O |
| Cádiz | Sanlucar de Barrameda | 36.46 N | 6.21 O |
| Cádiz | San Roque | 36.13 N | 5.23 O |
| Cádiz | Tarifa | 36.01 N | 5.37 O |
| Cádiz | Vejer de la Frontera | 36.15 N | 5.58 O |
| Fuerteventura | Puerto del Rosario | 28.30 N | 13.53 O |
| Gomera, La | San Sebastian de la Gomera | 28.05 N | 17.08 O |
| Gran Canaria | Arucas | 28.07 N | 15.31 O |
| Gran Canaria | Guia | 28.08 N | 15.40 O |
| Gran Canaria | Maspalomas | 27.46 N | 15.35 O |
| Gran Canaria | Las Palmas de Gran Canaria | 28.06 N | 15.25 O |
| Gran Canaria | San Bartolome de Tirajana | 27.56 N | 15.35 O |
| Gran Canaria | Telde | 27.58 N | 15.25 O |
| Hierro | Valverde | 27.48 N | 17.54 O |
| Lanzarote | Arrecife | 29.00 N | 13.34 O |
| Palma, La | Santa Cruz de la Palma | 28.41 N | 17.45 O |
| Palma, La | Los Llanos | 28.40 N | 17.56 O |
| Tenerife | Granadilla de Abona | 28.07 N | 16.35 O |
| Tenerife | Icod de los Vinos | 28.22 N | 16.43 O |
| Tenerife | Puerto de la Cruz | 28.25 N | 16.33 O |
| Tenerife | Santa Cruz de Tenerife | 28.28 N | 16.15 O |
| Castellón | Albocasser | 40.21 N | 0.01 E |
| Castellón | Alcala de Chivert | 40.19 N | 0.13 E |
| Castellón | Borriana | 39.53 N | 0.05 O |
| Castellón | Castellon de la Plana | 39.59 N | 0.02 O |
| Castellón | Lucena del Cid | 40.09 N | 0.17 O |
| Castellón | Morella | 40.37 N | 0.06 O |
| Castellón | Nules | 39.51 N | 0.09 O |
| Castellón | Onda | 39.58 N | 0.15 O |
| Castellón | Oropesa | 40.06 N | 0.09 E |
| Castellón | San Mateo | 40.28 N | 0.11 E |
| Castellón | Segorbe | 39.51 N | 0.29 O |
| Castellón | Villarreal de los Infantes | 39.56 N | 0.06 O |
| Castellón | Vinaroz | 40.28 N | 0.29 E |
| Castellón | Viver | 39.55 N | 0.36 O |
| Ciudad Real | Alcazar de San Juan | 39.24 N | 3.12 O |
| Ciudad Real | Almaden | 38.47 N | 4.50 O |
| Ciudad Real | Almagro | 38.53 N | 3.43 O |
| Ciudad Real | Almodovar del Campo | 38.42 N | 4.11 O |
| Ciudad Real | Ciudad Real | 38.59 N | 3.55 O |
| Ciudad Real | Daimiel | 39.05 N | 3.37 O |
| Ciudad Real | Malagon | 39.11 N | 3.52 O |
| Ciudad Real | Manzanares | 39.00 N | 3.22 O |
| Ciudad Real | Piedrabuena | 39.02 N | 4.10 O |
| Ciudad Real | Puertollano | 38.42 N | 4.07 O |
| Ciudad Real | Santa Cruz de Mudela | 38.39 N | 3.28 O |
| Ciudad Real | Socuellanos | 39.17 N | 2.47 O |
| Ciudad Real | Tomelloso | 39.10 N | 3.02 O |
| Ciudad Real | Valdepeñas | 38.46 N | 3.25 O |
| Ciudad Real | Villanueva de los Infantes | 38.44 N | 3.01 O |
| Cordoba | Aguilar | 37.31 N | 4.39 O |
| Cordoba | Baena | 37.37 N | 4.20 O |
| Cordoba | Bujalance | 37.54 N | 4.23 O |
| Cordoba | Cabra | 37.28 N | 4.26 O |
| Cordoba | Castro del Rio | 37.41 N | 4.29 O |
| Cordoba | Cordoba | 37.53 N | 4.47 O |
| Cordoba | Fuente-Ovejuna | 38.16 N | 5.25 O |
| Cordoba | Hinojosa del Duque | 38.30 N | 5.09 O |
| Cordoba | Lucena | 37.24 N | 4.29 O |
| Cordoba | Montilla | 37.36 N | 4.38 O |
| Cordoba | Montoro | 38.01 N | 4.22 O |
| Cordoba | Palma del Rio | 37.42 N | 5.17 O |
| Cordoba | Peñarroya-Pueblonuevo | 38.19 N | 5.16 O |
| Cordoba | Posadas | 37.48 N | 5.07 O |
| Cordoba | Pozoblanco | 38.23 N | 4.51 O |
| Cordoba | Priego de Cordoba | 37.26 N | 4.12 O |
| Cordoba | Puente Genil | 37.23 N | 4.46 O |
| Cordoba | La Rambla | 37.37 N | 4.44 O |
| Cordoba | Rute | 37.19 N | 4.23 O |
| Coruña | Arzua | 42.53 N | 8.11 O |
| Coruña | Betanzos | 43.17 N | 8.13 O |
| Coruña | Carballo | 43.13 N | 8.41 O |
| Coruña | Corcubion | 42.56 N | 9.12 O |
| Coruña | Coruña | 43.22 N | 8.23 O |
| Coruña | El Ferrol | 43.29 N | 8.14 O |
| Coruña | Muros | 42.46 N | 9.05 O |
| Coruña | Negreira | 42.54 N | 8.45 O |
| Coruña | Noya | 42.48 N | 8.53 O |
| Coruña | Ordenes | 43.05 N | 8.24 O |
| Coruña | Padron | 42.44 N | 8.39 O |
| Coruña | Pontedeume | 43.24 N | 8.10 O |
| Coruña | Puentes de Garcia Rodriguez | 43.27 N | 7.51 O |
| Coruña | Ribeira | 42.34 N | 8.59 O |
| Coruña | Santa Maria de Ortigueira | 43.41 N | 7.50 O |
| Coruña | Santiago de Compostela | 42.52 N | 8.33 O |
| Cuenca | Belmonte | 39.34 N | 2.43 O |
| Cuenca | Cañete | 40.03 N | 1.40 O |
| Cuenca | Cuenca | 40.04 N | 2.08 O |
| Cuenca | Huete | 40.09 N | 2.43 O |
| Cuenca | Motilla del Palancar | 39.34 N | 1.54 O |
| Cuenca | San Clemente | 39.23 N | 2.24 O |
| Cuenca | Tarancon | 40.01 N | 3.01 O |
| Girona | Bañoles | 42.07 N | 2.46 E |
| Girona | Besalu | 42.12 N | 2.42 E |
| Girona | La Bisbal | 41.58 N | 3.02 E |
| Girona | Blanes | 41.40 N | 2.48 E |
| Girona | Camprodon | 42.19 N | 2.22 E |
| Girona | Figueres | 42.16 N | 2.58 E |
| Girona | Girona | 41.59 N | 2.49 E |
| Girona | Llanga | 42.21 N | 3.10 E |
| Girona | Olot | 42.11 N | 2.30 E |
| Girona | Palafrugell | 41.55 N | 3.10 E |
| Girona | Palamos | 41.51 N | 3.08 E |
| Girona | Puigcerda | 42.26 N | 1.56 E |
| Girona | Ripoll | 42.12 N | 2.12 E |
| Girona | Roses | 42.16 N | 3.11 E |
| Girona | Sant Feliu de Guixols | 41.47 N | 3.02 E |
| Girona | Santa Coloma de Farnés | 41.52 N | 2.40 E |
| Girona | Santa Pau | 42.09 N | 2.35 E |
| Girona | Sarriá de Ter | 42.01 N | 2.49 E |
| Granada | Albuñol | 36.48 N | 3.12 O |
| Granada | Alhama de Granada | 37.00 N | 3.59 O |
| Granada | Almuñecar | 36.44 N | 3.41 O |
| Granada | Baza | 37.30 N | 2.46 O |
| Granada | Granada | 37.11 N | 3.35 O |
| Granada | Guadix | 37.18 N | 3.09 O |
| Granada | Huescar | 37.48 N | 2.33 O |
| Granada | Iznalloz | 37.24 N | 3.32 O |
| Granada | Loja | 37.10 N | 4.10 O |
| Granada | Montefrio | 37.20 N | 4.00 O |
| Granada | Motril | 36.44 N | 3.31 O |
| Granada | Orgiva | 36.54 N | 3.26 O |
| Granada | Pinos Puente | 37.15 N | 3.45 O |
| Granada | Santa Fé | 37.11 N | 3.43 O |
| Granada | Ugijar | 36.58 N | 3.03 O |
| Guadalajara | Atienza | 41.12 N | 2.52 O |
| Guadalajara | Brihuega | 40.46 N | 2.52 O |
| Guadalajara | Cifuentes | 40.47 N | 2.37 O |
| Guadalajara | Cogolludo | 40.57 N | 3.05 O |
| Guadalajara | Guadalajara | 40.38 N | 3.10 O |
| Guadalajara | Molina de Aragón | 40.51 N | 1.53 O |
| Guadalajara | Pastrana | 40.25 N | 2.55 O |
| Guadalajara | Sacedón | 40.29 N | 2.44 O |
| Guadalajara | Siguenza | 41.04 N | 2.39 O |
| Guipuzcoa | Azpeitia | 43.13 N | 2.14 O |
| Guipuzcoa | Beasain | 43.03 N | 2.12 O |
| Guipuzcoa | Deva | 43.18 N | 2.21 O |
| Guipuzcoa | Eibar | 43.11 N | 2.28 O |
| Guipuzcoa | Hernani | 43.18 N | 1.54 O |
| Guipuzcoa | Irún | 43.20 N | 1.47 O |
| Guipuzcoa | Mondragón | 43.05 N | 2.30 O |
| Guipuzcoa | Renteria | 43.17 N | 1.58 O |
| Guipuzcoa | San Sebastián | 43.19 N | 1.59 O |
| Guipuzcoa | Tolosa | 43.08 N | 2.05 O |
| Guipuzcoa | Vergara | 43.07 N | 2.25 O |
| Guipuzcoa | Zarauz | 43.17 N | 2.10 O |
| Huelva | Aracena | 37.54 N | 6.33 O |
| Huelva | Ayamonte | 37.13 N | 7.24 O |
| Huelva | Huelva | 37.16 N | 6.57 O |
| Huelva | Jabugo | 37.55 N | 6.44 O |
| Huelva | Moguer | 37.17 N | 6.51 O |
| Huelva | Palma del Condado | 37.23 N | 6.35 O |
| Huelva | Puebla de Guzmán | 37.37 N | 7.15 O |
| Huelva | Valverde del Camino | 37.35 N | 6.45 O |
| Huesca | Ainsa | 42.25 N | 0.09 E |
| Huesca | Ayerbe | 42.17 N | 0.42 O |
| Huesca | Barbastro | 42.02 N | 0.08 E |
| Huesca | Benabarre | 42.07 N | 0.29 E |
| Huesca | Benasque | 42.37 N | 0.31 E |
| Huesca | Biescas | 42.38 N | 0.09 O |
| Huesca | Boltaña | 42.27 N | 0.04 E |
| Huesca | Broto | 42.36 N | 0.08 O |
| Huesca | Canfranc | 42.42 N | 0.31 O |
| Huesca | Fraga | 41.32 N | 0.21 E |
| Huesca | Graus | 42.11 N | 0.20 E |
| Huesca | Huesca | 42.08 N | 0.24 O |
| Huesca | Jaca | 42.34 N | 0.33 O |
| Huesca | Monzón | 41.55 N | 0.11 E |
| Huesca | Sabiñánigo | 42.31 N | 0.22 O |
| Huesca | Sariñena | 41.47 N | 0.10 O |
| Huesca | Tamarite de Litera | 41.52 N | 0.25 E |
| Jaén | Alcalá la Real | 37.28 N | 3.56 O |
| Jaén | Alcaudete | 37.35 N | 4.05 O |
| Jaén | Andújar | 38.02 N | 4.03 O |
| Jaén | Baeza | 38.00 N | 3.28 O |
| Jaén | Bailén | 38.06 N | 3.46 O |
| Jaén | Beas de Segura | 38.15 N | 2.53 O |
| Jaén | La Carolina | 38.17 N | 3.37 O |
| Jaén | Cazorla | 37.55 N | 3.00 O |
| Jaén | Jaén | 37.46 N | 3.47 O |
| Jaén | Huelma | 37.39 N | 3.28 O |
| Jaén | Jódar | 37.50 N | 3.21 O |
| Jaén | Linares | 38.06 N | 3.38 O |
| Jaén | Mancha Real | 37.47 N | 3.37 O |
| Jaén | Martos | 37.44 N | 3.58 O |
| Jaén | Mengibar | 37.58 N | 3.48 O |
| Jaén | Orcera | 38.19 N | 2.39 O |
| Jaén | Porcuna | 37.52 N | 4.11 O |
| Jaén | Quesada | 37.51 N | 3.05 O |
| Jaén | Ubeda | 38.01 N | 3.23 O |
| Jaén | Villacarrillo | 38.07 N | 3.05 O |
| León | Astorga | 42.27 N | 6.09 O |
| León | La Bañeza | 42.17 N | 5.52 O |
| León | Cistierna | 42.48 N | 5.08 O |
| León | León | 42.36 N | 5.34 O |
| León | Murias de Paredes | 42.52 N | 6.11 O |
| León | Ponferrada | 42.33 N | 6.35 O |
| León | Riaño | 42.59 N | 5.00 O |
| León | Sahagún | 42.22 N | 5.02 O |
| León | Valencia de Don Juan | 42.17 N | 5.31 O |
| León | La Vecilla | 42.51 N | 5.25 O |
| León | Villablino | 42.56 N | 6.19 O |
| León | Villafranca del Bierzo | 42.37 N | 6.49 O |
| Logroño | Alfaro | 42.10 N | 1.45 O |
| Logroño | Arnedo | 42.14 N | 2.05 O |
| Logroño | Calahorra | 42.18 N | 1.59 O |
| Logroño | Cervera del Rio Alhama | 42.02 N | 1.58 O |
| Logroño | Haro | 42.36 N | 2.48 O |
| Logroño | Logroño | 42.28 N | 2.27 O |
| Logroño | Nájera | 42.25 N | 2.45 O |
| Logroño | Santo Domingo de la Calzada | 42.26 N | 2.57 O |
| Logroño | Torrecilla en Cameros | 42.15 N | 2.37 O |
| Lugo | Becerrea | 42.51 N | 7.10 O |
| Lugo | Chantada | 42.36 N | 7.46 O |
| Lugo | Fonsagrada | 43.08 N | 7.04 O |
| Lugo | Lugo | 43.01 N | 7.33 O |
| Lugo | Mondoñedo | 43.25 N | 7.23 O |
| Lugo | Monforte de Lemos | 42.31 N | 7.30 O |
| Lugo | Quiroga | 42.28 N | 7.15 O |
| Lugo | Ribadeo | 43.32 N | 7.03 O |
| Lugo | Sarria | 42.47 N | 7.25 O |
| Lugo | Villalba | 43.17 N | 7.41 O |
| Lugo | Vivero | 43.39 N | 7.38 O |
| Lleida | Ager | 42.00 N | 0.45 E |
| Lleida | Agramunt | 41.47 N | 1.06 E |
| Lleida | Artese de Segre | 41.54 N | 1.03 E |
| Lleida | Balaguer | 41.47 N | 0.48 E |
| Lleida | Borges Blanques | 41.31 N | 0.52 E |
| Lleida | Cervera | 41.41 N | 1.16 E |
| Lleida | Esterri d'Aneu | 42.38 N | 1.08 E |
| Lleida | Lleida | 41.37 N | 0.38 E |
| Lleida | Pobla de Segur | 42.15 N | 0.58 E |
| Lleida | Pont de Suert | 42.25 N | 0.45 E |
| Lleida | La Seu d'Urgell | 42.22 N | 1.28 E |
| Lleida | Solsona | 42.00 N | 1.31 E |
| Lleida | Sort | 42.25 N | 1.08 E |
| Lleida | Tárrega | 41.39 N | 1.09 E |
| Lleida | Tremp | 42.10 N | 0.54 E |
| Lleida | Viella | 42.42 N | 0.48 E |
| Madrid | Alcobendas | 40.32 N | 3.38 O |
| Madrid | Alcorcón | 40.20 N | 3.50 O |
| Madrid | Alcalá de Henares | 40.28 N | 3.22 O |
| Madrid | Aranjuez | 40.01 N | 3.38 O |
| Madrid | Arganda | 40.19 N | 3.26 O |
| Madrid | Collado Villalba | 40.36 N | 3.59 O |
| Madrid | Colmenar Viejo | 40.39 N | 3.47 O |
| Madrid | Chinchón | 40.08 N | 3.26 O |
| Madrid | Fuenlabrada | 40.17 N | 3.48 O |
| Madrid | Getafe | 40.18 N | 3.44 O |
| Madrid | Leganés | 40.19 N | 3.46 O |
| Madrid | Madrid | 40.24 N | 3.41 O |
| Madrid | Móstoles | 40.20 N | 3.52 O |
| Madrid | Navalcarnero | 40.17 N | 4.01 O |
| Madrid | Pinto | 40.14 N | 3.43 O |
| Madrid | San Lorenzo del Escorial | 40.35 N | 4.05 O |
| Madrid | San Martin de Valdeiglesias | 40.21 N | 4.24 O |
| Madrid | Torrejón de Ardoz | 40.27 N | 3.29 O |
| Madrid | Torrelaguna | 40.50 N | 3.35 O |
| Málaga | Alora | 36.49 N | 4.42 O |
| Málaga | Antequera | 37.01 N | 4.33 O |
| Málaga | Archidona | 37.06 N | 4.23 O |
| Málaga | Campillos | 37.03 N | 4.51 O |
| Málaga | Coin | 36.40 N | 4.46 O |
| Málaga | Colmenar | 36.54 N | 4.20 O |
| Málaga | Estepona | 36.25 N | 5.09 O |
| Málaga | Fuengirola | 36.32 N | 4.38 O |
| Málaga | Gaucin | 36.31 N | 5.19 O |
| Málaga | Marbella | 36.30 N | 4.54 O |
| Málaga | Málaga | 36.43 N | 4.25 O |
| Málaga | Nerja | 36.44 N | 3.53 O |
| Málaga | Ronda | 36.45 N | 5.10 O |
| Málaga | Torremolinos | 36.38 N | 4.30 O |
| Málaga | Torrox | 36.46 N | 3.57 O |
| Málaga | Vélez Málaga | 36.47 N | 4.05 O |
| Murcia | Aguilas | 37.24 N | 1.35 O |
| Murcia | Caravaca | 38.08 N | 1.52 O |
| Murcia | Cartagena | 37.36 N | 0.59 O |
| Murcia | Cieza | 38.15 N | 1.25 O |
| Murcia | Jumilla | 38.29 N | 1.20 O |
| Murcia | Lorca | 37.41 N | 1.42 O |
| Murcia | Molina de Segura | 38.03 N | 1.13 O |
| Murcia | Mula | 38.03 N | 1.30 O |
| Murcia | Murcia | 37.59 N | 1.07 O |
| Murcia | San Javier | 37.49 N | 0.50 O |
| Murcia | Totana | 37.46 N | 1.30 O |
| Murcia | Yecla | 38.37 N | 1.07 O |
| Navarra | Alsasua | 42.54 N | 2.10 O |
| Navarra | Aoiz | 42.46 N | 1.22 O |
| Navarra | Estella | 42.40 N | 2.02 O |
| Navarra | Pamplona | 42.49 N | 1.38 O |
| Navarra | Puente de la Reina | 42.40 N | 1.49 O |
| Navarra | Roncal | 42.50 N | 0.55 O |
| Navarra | Roncesvalles | 43.01 N | 1.20 O |
| Navarra | Sangüesa | 42.35 N | 1.17 O |
| Navarra | Tafalla | 42.30 N | 1.42 O |
| Navarra | Tudela | 42.04 N | 1.36 O |
| Ourense | Allariz | 42.11 N | 7.50 O |
| Ourense | Bande | 42.03 N | 7.58 O |
| Ourense | El Barco de Valdorras | 42.25 N | 6.59 O |
| Ourense | Carballino | 42.26 N | 8.05 O |
| Ourense | Celanova | 42.09 N | 7.58 O |
| Ourense | Guinzo de Limia | 42.03 N | 7.44 O |
| Ourense | Orense | 42.20 N | 7.52 O |
| Ourense | Puebla de Trives | 42.20 N | 7.15 O |
| Ourense | Ribadavia | 42.17 N | 8.08 O |
| Ourense | Verin | 41.57 N | 7.27 O |
| Ourense | Viana del Bollo | 42.11 N | 7.07 O |
| Palencia | Aguilar del Campoo | 42.48 N | 4.15 O |
| Palencia | Astudillo | 42.12 N | 4.17 O |
| Palencia | Baltanás | 41.56 N | 4.15 O |
| Palencia | Venta de Baños | 41.56 N | 4.30 O |
| Palencia | Carrión de los Condes | 42.20 N | 4.36 O |
| Palencia | Cervera del Pisuerga | 42.51 N | 4.30 O |
| Palencia | Frechilla | 42.09 N | 4.50 O |
| Palencia | Herrera del Pisuerga | 42.35 N | 4.20 O |
| Palencia | Palencia | 42.00 N | 4.32 O |
| Palencia | Saldaña | 42.32 N | 4.44 O |
| Pontevedra | Caldas de Reyes | 42.36 N | 8.39 O |
| Pontevedra | Cambados | 42.31 N | 8.49 O |
| Pontevedra | La Cañiza | 42.13 N | 8.16 O |
| Pontevedra | La Estrada | 42.42 N | 8.29 O |
| Pontevedra | La Guardia | 41.56 N | 8.52 O |
| Pontevedra | Lalin | 42.40 N | 8.07 O |
| Pontevedra | Pontevedra | 42.26 N | 8.39 O |
| Pontevedra | Porriño | 42.12 N | 8.39 O |
| Pontevedra | Puenteáreas | 42.10 N | 8.28 O |
| Pontevedra | Redondela | 42.17 N | 8.37 O |
| Pontevedra | Sangenjo | 42.24 N | 8.48 O |
| Pontevedra | Tuy | 42.03 N | 8.39 O |
| Pontevedra | Vigo | 42.15 N | 8.43 O |
| Pontevedra | Villagarcia de Arosa | 42.36 N | 8.46 O |
| Salamanca | Alba de Tormes | 40.50 N | 5.30 O |
| Salamanca | Béjar | 40.23 N | 5.46 O |
| Salamanca | Ciudad Rodrigo | 40.36 N | 6.32 O |
| Salamanca | Guijuelo | 40.33 N | 5.40 O |
| Salamanca | Ledesma | 41.05 N | 5.59 O |
| Salamanca | Lumbrales | 40.56 N | 6.43 O |
| Salamanca | Peñaranda de Bracamonte | 40.54 N | 5.13 O |
| Salamanca | Salamanca | 40.57 N | 5.40 O |
| Salamanca | Sequeros | 40.31 N | 6.02 O |
| Salamanca | Vitigudino | 41.01 N | 6.26 O |
| Santander | Cabuérniga | 43.14 N | 4.18 O |
| Santander | Castro Urdiales | 43.23 N | 3.13 O |
| Santander | Laredo | 43.26 N | 3.28 O |
| Santander | Potes | 43.10 N | 4.37 O |
| Santander | Ramales de la Victoria | 43.15 N | 3.28 O |
| Santader | Reinosa | 43.00 N | 4.08 O |
| Santander | Santander | 43.28 N | 3.48 O |
| Santander | Santoña | 43.27 N | 3.29 O |
| Santander | San Vicente de la Barquera | 43.24 N | 4.24 O |
| Santander | Torrelavega | 43.20 N | 4.02 O |
| Santander | Villacarriedo | 43.14 N | 3.48 O |
| Segovia | Cuéllar | 41.23 N | 4.21 O |
| Segovia | Riaza | 41.18 N | 3.30 O |
| Segovia | Santa Maria la Real de Nieva | 41.04 N | 4.24 O |
| Segovia | Segovia | 40.57 N | 4.07 O |
| Segovia | Sepúlveda | 41.18 N | 3.43 O |
| Segovia | Villacastin | 40.47 N | 4.25 O |
| Sevilla | Alcalá de Guadaira | 37.20 N | 5.50 O |
| Sevilla | Alcalá del Rio | 37.31 N | 5.58 O |
| Sevilla | Almadén de la Plata | 37.52 N | 6.04 O |
| Sevilla | Carmona | 37.28 N | 5.38 O |
| Sevilla | Cazalla de la Sierra | 37.56 N | 5.45 O |
| Sevilla | Coria del Rio | 37.18 N | 6.04 O |
| Sevilla | Dos Hermanas | 37.17 N | 5.55 O |
| Sevilla | Ecija | 37.32 N | 5.05 O |
| Sevilla | Estepa | 37.17 N | 4.52 O |
| Sevilla | Lebrija | 36.55 N | 6.05 O |
| Sevilla | Lora del Rio | 37.39 N | 5.32 O |
| Sevilla | Marchena | 37.20 N | 5.26 O |
| Sevilla | Morón de la Frontera | 37.07 N | 5.28 O |
| Sevilla | Osuna | 37.14 N | 5.07 O |
| Sevilla | Los Palacios y Villafranca | 37.10 N | 5.55 O |
| Sevilla | Sanlúcar La Mayor | 37.24 N | 6.12 O |
| Sevilla | Sevilla | 37.23 N | 5.59 O |
| Sevilla | Utrera | 37.11 N | 5.46 O |
| Soria | Agreda | 41.49 N | 1.54 O |
| Soria | Almazán | 41.29 N | 2.32 O |
| Soria | El Burgo de Osma | 41.35 N | 3.04 O |
| Soria | Medinaceli | 41.11 N | 2.26 O |
| Soria | Soria | 41.46 N | 2.28 O |
| Tarragona | Amposta | 40.23 N | 0.34 E |
| Tarragona | Ascó | 41.11 N | 0.34 E |
| Tarragona | Falset | 41.09 N | 0.50 E |
| Tarragona | Gandesa | 41.03 N | 0.26 E |
| Tarragona | Montblanc | 41.23 N | 1.10 E |
| Tarragona | Mora d'Ebre | 41.06 N | 0.38 E |
| Tarragona | Perelló | 40.52 N | 0.43 E |
| Tarragona | Reus | 41.10 N | 1.06 E |
| Tarragona | Santa Bárbara | 40.43 N | 0.30 E |
| Tarragona | Tarragona | 41.07 N | 1.16 E |
| Tarragona | Tortosa | 40.49 N | 0.31 E |
| Tarragona | Valls | 41.17 N | 1.15 E |
| Tarragona | Vendrell | 41.13 N | 1.32 E |
| Teruel | Albarracin | 40.25 N | 1.27 O |
| Teruel | Alcañiz | 41.02 N | 0.08 O |
| Teruel | Aliaga | 40.40 N | 0.42 O |
| Teruel | Calamocha | 40.55 N | 1.17 O |
| Teruel | Calanda | 40.56 N | 0.14 O |
| Teruel | Castellote | 40.48 N | 0.20 O |
| Teruel | Hijar | 41.10 N | 0.27 O |
| Teruel | Montalbán | 40.50 N | 0.48 O |
| Teruel | Monreal del Campo | 40.47 N | 1.20 O |
| Teruel | Mora de Rubielos | 40.15 N | 0.45 O |
| Teruel | Muniesa | 41.02 N | 0.49 O |
| Teruel | Teruel | 40.20 N | 1.06 O |
| Teruel | Torrijas | 40.02 N | 0.57 O |
| Teruel | Valderrobles | 40.52 N | 0.10 E |
| Toledo | Escalona | 40.09 N | 4.24 O |
| Toledo | Illescas | 40.08 N | 3.51 O |
| Toledo | Madridejos | 39.28 N | 3.33 O |
| Toledo | Navahermosa | 39.39 N | 4.28 O |
| Toledo | Ocaña | 39.57 N | 3.30 O |
| Toledo | Orgaz | 39.39 N | 3.53 O |
| Toledo | El Puente del Arzobispo | 39.48 N | 5.10 O |
| Toledo | Quintanar de la Orden | 39.35 N | 3.03 O |
| Toledo | Talavera de la Reina | 39.58 N | 4.50 O |
| Toledo | Toledo | 39.51 N | 4.01 O |
| Toledo | Torrijos | 39.59 N | 4.17 O |
| Valencia | Albaida | 38.51 N | 0.31 O |
| Valencia | Alberique | 39.07 N | 0.31 O |
| Valencia | Alcira | 39.09 N | 0.26 O |
| Valencia | Algemesi | 39.12 N | 0.26 O |
| Valencia | Ayora | 39.03 N | 1.03 O |
| Valencia | Benifayó | 39.17 N | 0.25 O |
| Valencia | Burjassot | 39.30 N | 0.25 O |
| Valencia | Carcaixent | 39.08 N | 0.28 O |
| Valencia | Carlet | 39.14 N | 0.31 O |
| Valencia | Catarroja | 39.24 N | 0.24 O |
| Valencia | Cofrentes | 39.13 N | 1.04 O |
| Valencia | Cullera | 39.10 N | 0.15 O |
| Valencia | Chelva | 39.45 N | 1.00 O |
| Valencia | Chiva | 39.28 N | 0.43 O |
| Valencia | Enguera | 38.59 N | 0.40 O |
| Valencia | Gandia | 38.58 N | 0.11 O |
| Valencia | Liria | 39.37 N | 0.36 O |
| Valencia | Manises | 39.29 N | 0.28 O |
| Valencia | Massamagrell | 39.34 N | 0.20 O |
| Valencia | Oliva | 38.55 N | 0.07 O |
| Valencia | Onteniente | 38.50 N | 0.36 O |
| Valencia | Paterna | 39.30 N | 0.26 O |
| Valencia | Requena | 39.30 N | 1.06 O |
| Valencia | Sagunto | 39.41 N | 0.16 O |
| Valencia | Silla | 39.22 N | 0.24 O |
| Valencia | Sueca | 39.12 N | 0.20 O |
| Valencia | Torrent de l'Horta | 39.26 N | 0.28 O |
| Valencia | Utiel | 39.34 N | 1.12 O |
| Valencia | Valencia | 39.28 N | 0.22 O |
| Valencia | Villar del Arzobispo | 39.44 N | 0.50 O |
| Valencia | Xátiva | 39.00 N | 0.31 O |
| Valladolid | Medina de Rioseco | 41.53 N | 5.03 O |
| Valladolid | Medina del Campo | 41.18 N | 4.55 O |
| Valladolid | Mota del Marqués | 41.38 N | 5.11 O |
| Valladolid | Nava del Rey | 41.20 N | 5.05 O |
| Valladolid | Olmedo | 41.17 N | 4.41 O |
| Valladolid | Peñafiel | 41.36 N | 4.07 O |
| Valladolid | Tordesillas | 41.30 N | 5.00 O |
| Valladolid | Valoria la Buena | 41.48 N | 4.32 O |
| Valladolid | Valladolid | 41.39 N | 4.44 O |
| Valladolid | Villalón de Campos | 42.06 N | 5.02 O |
| Vizcaya | Baracaldo | 43.20 N | 2.57 O |
| Vizcaya | Bermeo | 43.25 N | 2.44 O |
| Vizcaya | Bilbao | 43.15 N | 2.55 O |
| Vizcaya | Durango | 43.13 N | 2.40 O |
| Vizcaya | Guernica | 43.19 N | 2.40 O |
| Vizcaya | Marquina | 43.18 N | 2.30 O |
| Vizcaya | Valmaseda | 43.12 N | 3.14 O |
| Zamora | Alcañices | 41.42 N | 6.21 O |
| Zamora | Benavente | 42.00 N | 5.41 O |
| Zamora | Bermillo de Sayago | 41.22 N | 6.07 O |
| Zamora | Fuentesaúco | 41.14 N | 5.30 O |
| Zamora | Puebla de Sanabria | 42.03 N | 6.39 O |
| Zamora | Toro | 41.31 N | 5.24 O |
| Zamora | Villalpando | 41.52 N | 5.25 O |
| Zamora | Zamora | 41.30 N | 5.45 O |
| Zaragoza | La Almunia de Doña Godina | 41.29 N | 1.23 O |
| Zaragoza | Ariza | 41.19 N | 2.03 O |
| Zaragoza | Ateca | 41.20 N | 1.48 O |
| Zaragoza | Belchite | 41.18 N | 0.45 O |
| Zaragoza | Borja | 41.49 N | 1.32 O |
| Zaragoza | Bujaraloz | 41.29 N | 0.10 O |
| Zaragoza | Calatayud | 41.21 N | 1.38 O |
| Zaragoza | Cariñena | 41.20 N | 1.13 O |
| Zaragoza | Caspe | 41.14 N | 0.02 O |
| Zaragoza | Daroca | 41.07 N | 1.25 O |
| Zaragoza | Egea de los Caballeros | 42.07 N | 1.09 O |
| Zaragoza | Escatrón | 41.17 N | 0.20 O |
| Zaragoza | Pina de Ebro | 41.29 N | 0.32 O |
| Zaragoza | Sádaba | 42.17 N | 1.16 O |
| Zaragoza | Sos del Rey Católico | 42.29 N | 1.12 O |
| Zaragoza | Tarazona | 41.54 N | 1.43 O |
| Zaragoza | Tauste | 41.56 N | 1.15 O |
| Zaragoza | Zaragoza | 41.39 N | 0.52 O |
| Zaragoza | Zuera | 41.52 N | 0.47 O |
| Coordenadas UTM de los Vértices Geodésicos españoles |
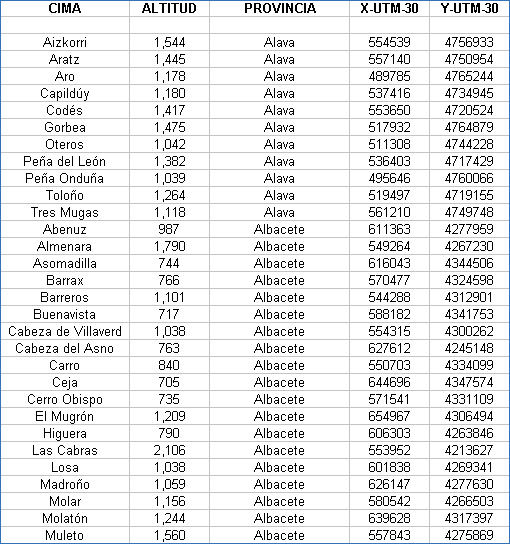

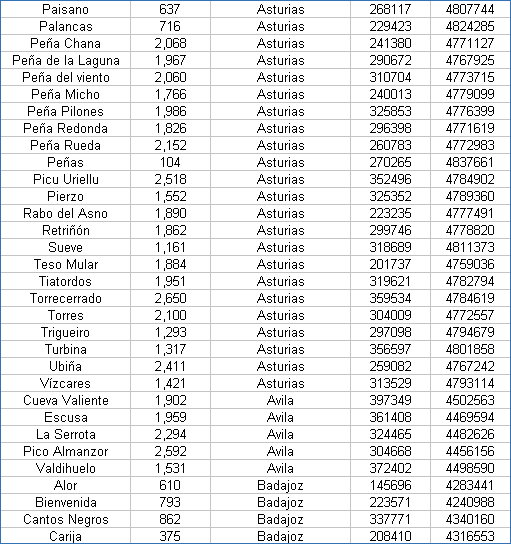
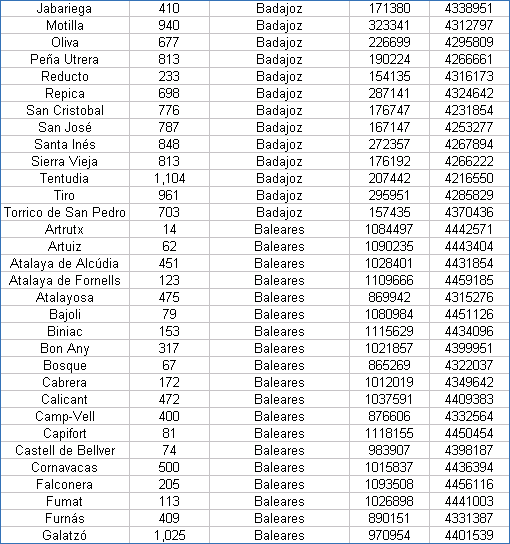
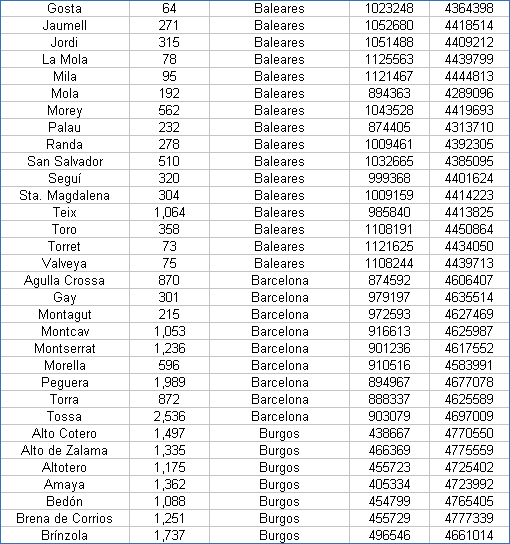
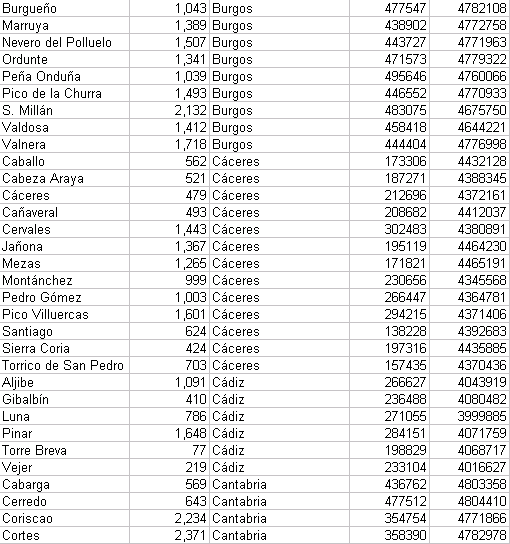
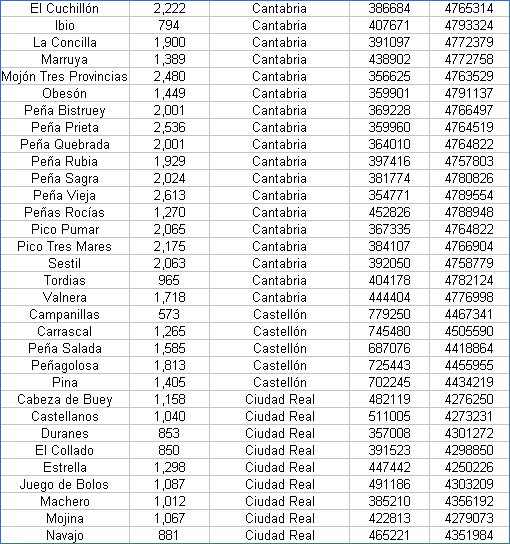

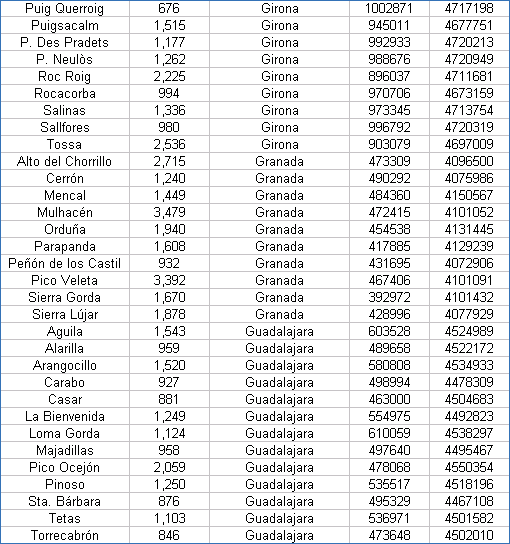

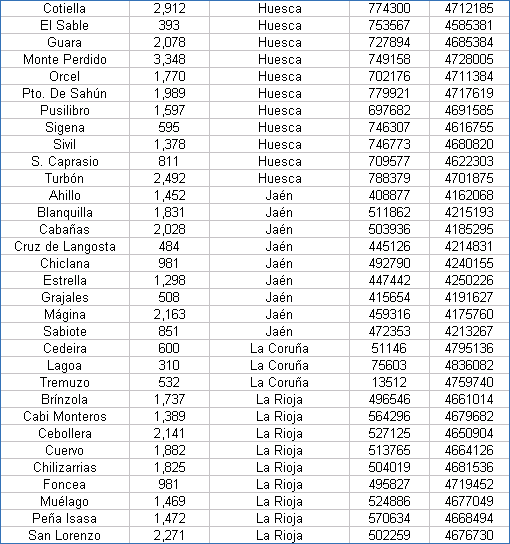
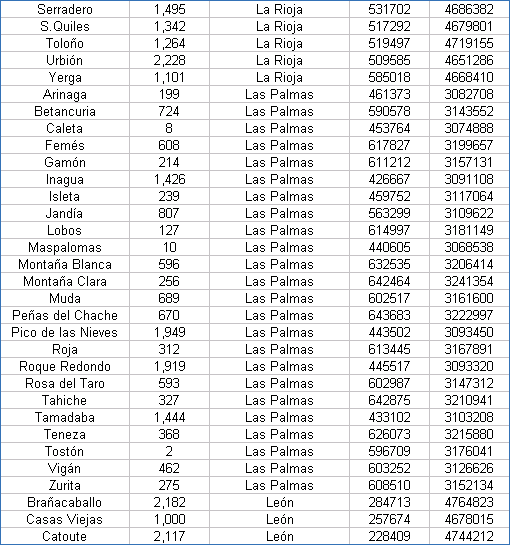
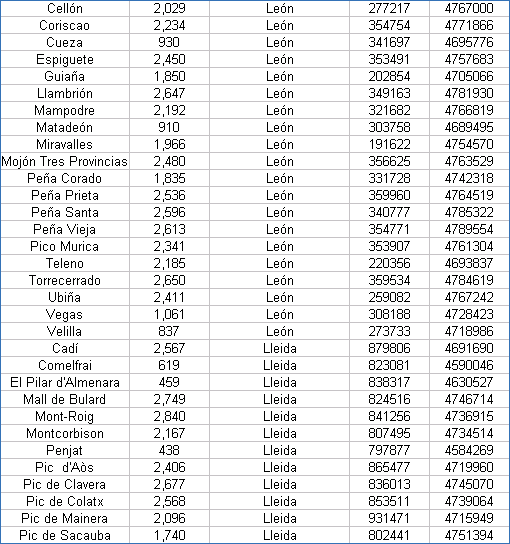
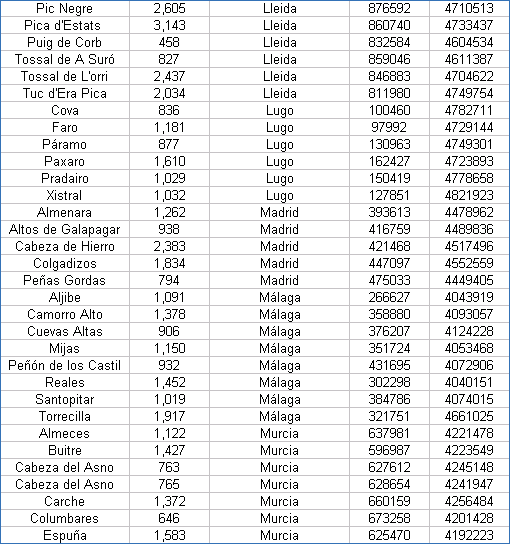
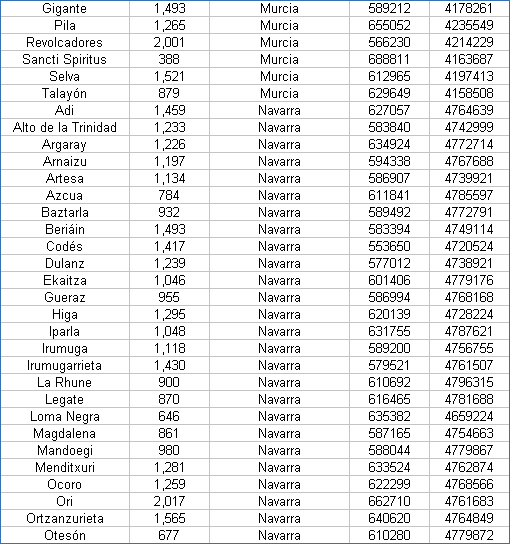
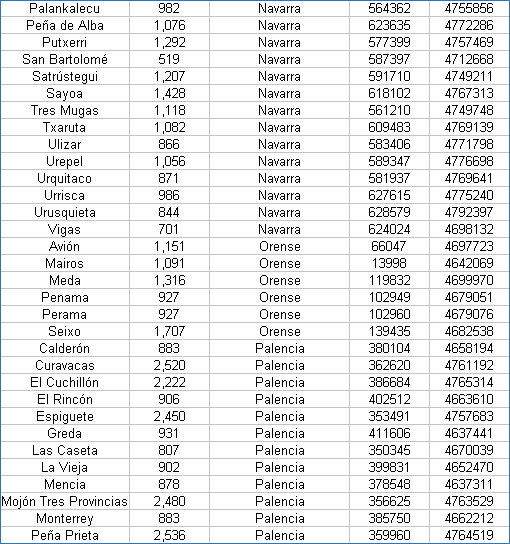

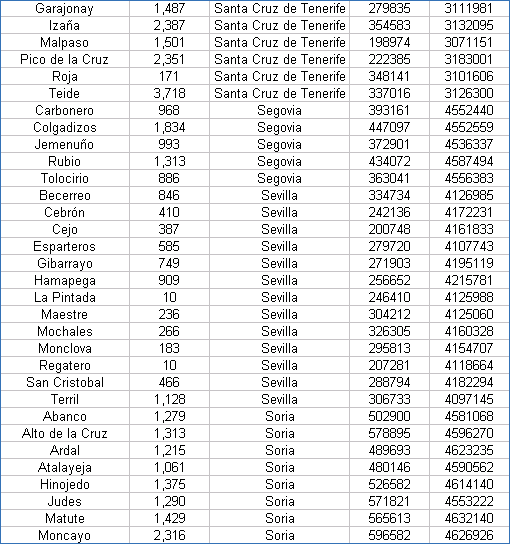
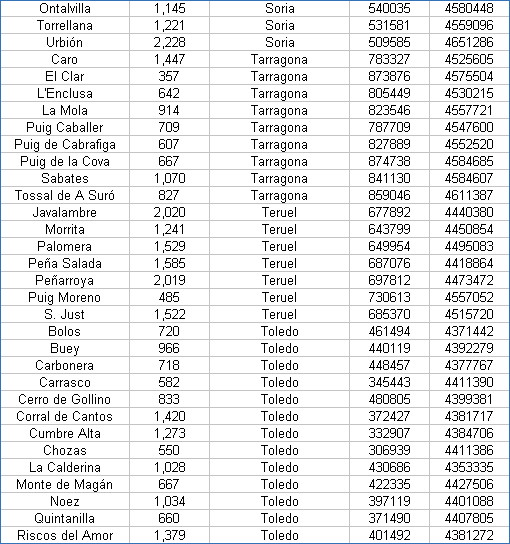

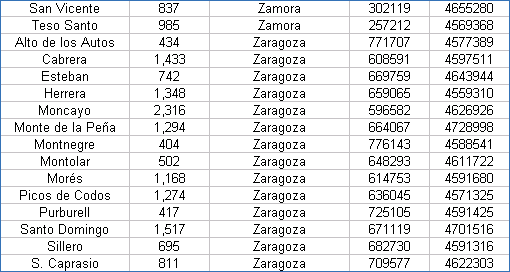
Las coordenadas están referidas al Datum European 50 y al huso 30. Hay que tener presente que las coordenadas exactas de los vértices geodésicos las suministra el IGN previo pago, por lo que estos valores han de tomarse con ciertas limitaciones.
| Nociones básicas sobre proyecciones cartográficas |
Conceptualmente una proyección cartográfica es una correspondencia biunívoca entre los puntos de la superficie terrestre y los puntos de un plano llamado Plano de proyección.
Puesto que cualquier punto de la esfera está definido por sus coordenadas geográficas (l,f) y cualquier punto del plano lo está por sus coordenadas cartesianas (X,Y), existirá una serie infinita de relaciones que liguen (l,f) con (X.Y). Cada una de estas infinitas relaciones será un sistema de proyección Cartográfico.
| Clasificación de las proyecciones |
PURAS |
||
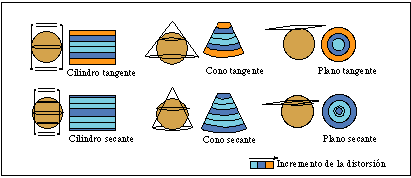
POR DESARROLLO Se proyecta la esfera sobre una superficie desarrollable que puede ser tangente o secante a la esfera. |
CÓNICAS |
Punto de vista en el centro de la esfera. El plano de proyección es un cono tangente o secante a la esfera. |
CILINDRICAS |
Punto de vista en el centro de la esfera. El plano de proyección es un cilindro tangente a la esfera a lo largo de un círculo máximo. |
|
ACIMUTALES Toda la superficie se proyecta sobre un único plano de proyección. |
ORTOGRÁFICAS |
Punto de vista en el infinito. |
ESCENOGRÁFICAS |
Punto de vista en un punto propio fuera de la esfera. |
|
ESTEREOGRÁFICAS |
Punto de vista en las antípodas del punto de tangencia del plano de proyección. |
|
GNOMÓNICAS |
Punto de vista en el centro de la esfera. |
|
| POLIEDRICAS
División de la superficie terrestre en trapecios esféricos. Plano de proyección tangente al punto medio del trapecio. Punto de vista o centro de proyección en el infinito. |
||
MODIFICADAS |
||
CILINDRICAS |
Cilindrica modificada de Mercator |
|
CÓNICAS |
Proyección de Bonne |
|
ACIMUTALES |
Equidistante de Postell |
|
| La proyección Lambert |
Imaginemos la tierra con sus paralelos y meridianos, en el polo Norte se juntarán todos los meridianos. Si estiramos este punto, siguiendo el eje N-S, los meridianos se estirarán conservando el ángulo, y los paralelos continuaran siendo curvos (ver figura) así formaremos unos triángulos isósceles de base curva.
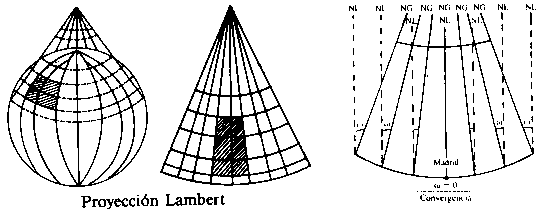
Al cuadricular los planos, perpendicular y paralelamente, determinando cuadrados de 1 Km 5. La meridiana geográfica y las líneas trazadas, originan un ángulo, este ángulo lo denominaremos, ángulo de convergencia o sencillamente convergencia. Y a las líneas verticales y paralelas entre si las denominaremos Lambert y cada una determina la dirección del N. Lambert.
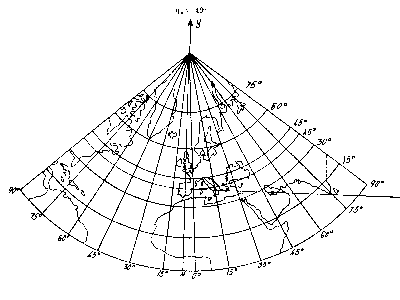
El cuadriculado Lambert es nacional; y el punto cero de convergencia o meridiano cero, pasa por el Observatorio Astronómico de Madrid, en este punto la meridiana geográfica y la Lambert es la misma, pero a medida que nos alejamos al E o al W de Madrid varía el ángulo de convergencia.
| La proyección U.T.M. |
La gran relación entre las naciones, en toda las ramas y aspectos, desde el comercial hasta el cultural, hace que los sistemas, códigos y demás elementos se unifiquen. A ello se tiende también en el campo de la cartofrafía. Los sistemas de proyección utilizados por los distintos países, o grupos de ellos, son varios. España, al igual que Bélgica, Dinamarca, Grecia, Rumania y Francia, utilizaban la proyección Lambert para representar sus territorios.
Después de la segunda guerra mundial los EE.UU. utilizan la proyección cilíndrica denominada Universal Tranversa Mercator, en siglas U.T.M., y gestionan hasta patrocinar su adopción universal.
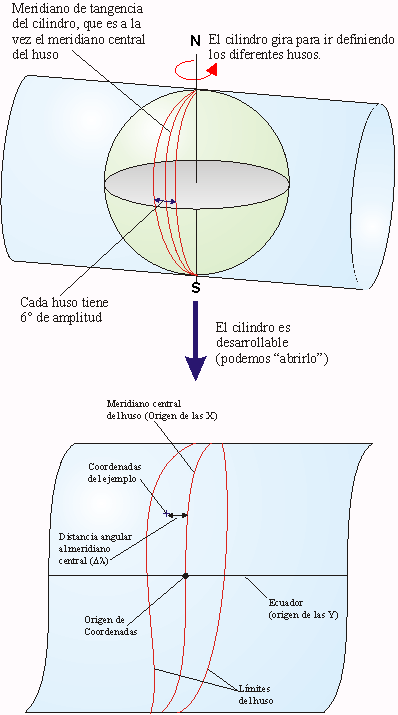
En la proyección UTM, se supone un cilindro tangente a un meridiano de la esfera terrestre, perpendicular al eje de la tierra y en el que el eje del cilindro, coincide con el de la Tierra (ver figura).
Los puntos del elipsoide terrestre se proyectan sobre el cilindro según una ley analítica. Al desarrollar el cilindro, el Ecuador queda representado por una recta, que se toma como eje de las XX, y el meridiano de tangencia se transforma en otra recta perpendicular a la anterior, que es el eje de las YY.
Este sistema (UTM), aplicado a grandes extensiones en longitud, hace que a medida que la representación se aleja del meridiano de tangencia, las deformaciones aumentan. Por ello se recurre al artificio de subdividir la superficie terrestre en 60 husos de 6E de amplitud, que constituyen 60 proyecciones iguales, pero referidas cada una al meridiano central del huso respectivo y al Ecuador.
| Cuadrícula U.T.M. (C.U.T.M.) |
Con la proyección cilíndrica obtenemos una serie de líneas verticales y horizontales, proyección de meridianos y paralelos que nos dan la cuadrícula del plano. Por trigonometría esférica se determina las intersecciones de meridianos con paralelos y con ellos se construye el canevas de la proyección.
Para la aplicación de esta cuadrícula universal y uniforme, basada en la proyección explicada, el sistema consiste en cubrir la superficie del globo comprendida entre los 80º de latitud Norte y los 80º de latitud Sur con un sistema homogéneo de cuadrícula UTM (CUTM). En planos de escala pequeña los meridianos y paralelos, constituyen la cuadrícula básica. En planos de mayor escala, estas líneas de referencia se complementan con otras.
| Descripción general de la cuadrícula U.T.M. (C.U.T.M.) |
En la proyección UTM la representación de la superficie terrestre por meridianos y paralelos se cubre, a su vez, por la CUTM entre las latitudes de +80 y -80, mediante paralelos múltiplos de 8. De este modo cada huso resulta compartimentado en 20 espacios o areas de 6º de longitud por 8º de latitud. Estos compartimentos se llaman zonas y forman la base de la C.U.T.M.
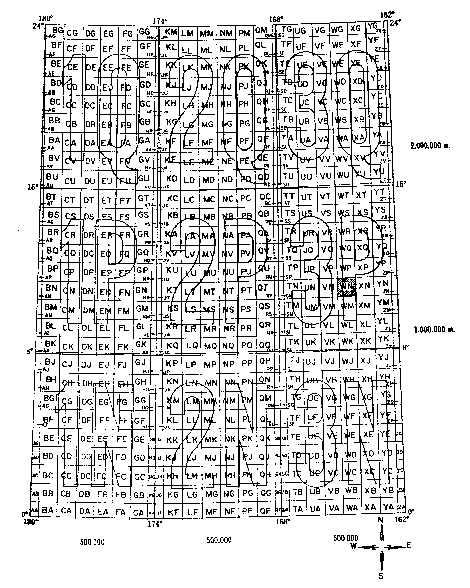
Plano básico de la C.U.T.M.
| Nomenclatura de las C.U.T.M. |
La numeración de los husos se hace correlativamente del 1 al 60, partiendo del antimeridiano de Greenwich y en sentido creciente hacia el E.
Las filas de zonas equidistantes del Ecuador son señaladas con letras mayúsculas, empezando por la A y hasta la X (se excluyen la I y la O), y con esta señalización se tiene ya la posibilidad de denominar todas las cuadrículas desde -80º (paralelo Sur) hasta +80º (paralelo Norte).
La designación de zona se hace leyendo primero el número del huso y después la letra.
La Zona de la C.U.T.M. cubre superficies de 10.000.000.000 m5.; cuadrados de 100.000 m. de lado, que se apoyan dentro de cada huso en los ejes de las YY (ordenadas) y al Ecuador como eje de las XX (abcisas).
La superficie de España, excluidas las Islas Canarias, esta comprendida en los husos 29, 30 y 31 y las filas de letras R, S y T, lo que supone el empleo de los tres husos citados con sus correspondientes C.U.T.M. y areas de superposición.
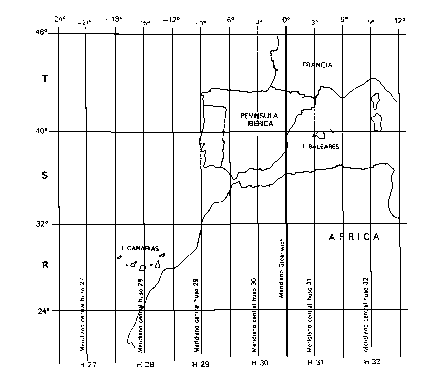
| Designación y numeración de las hojas |
Cada hoja del mapa se designa con dos números: el primero indica la columna a que pertenece y el segundo la fila.
Si queremos saber el número de la hoja situada al Norte o al Sur de otra dada, se restará o sumará al segundo grupo de números una unidad.
Si deseamos saber la numeración de una hoja situada al Este u Oeste de otra, se restará o sumará al primer grupo de cifras una unidad.
Para saber la numeración de una hoja situada al Noroeste (NW) de otra, se restará al primero y segundo grupo de cifras una unidad.
Para la numeración de las hojas situadas al Noreste (NE) de otra, se sumará una unidad al primer grupo de cifras y se restará una unidad al segundo grupo de cifras.
Para conocer la numeración de la hoja correspondiente al Suroeste (SW) de otra, se restará una unidad al primer grupo de cifras y se sumará al segundo grupo de cifras.
Y por fin, para determinar la numeración de la hoja situada al Sureste (SE) se sumará una unidad a cada uno de los grupos de cifras.
Estas reglas son validas para todas las hojas de las distintas escalas.
| Designación de un punto en los planos U.T.M. |
Se designarán los puntos por un grupo de letras y unos guarismos. Con el primer (o dos primeros) número, seguido de la correspondiente letra, se designa la zona del cuadrado establecido (Ej. 3OT). Con el grupo siguiente de dos letras se designa el cuadrado de 100 Km. (Ej. UK). Con el siguiente grupo de varios guarismos, la ordenada y con el siguiente la abcisa (Ej. 963-785).
Con lo que el punto quedará así asignado: 3OTUK936785.
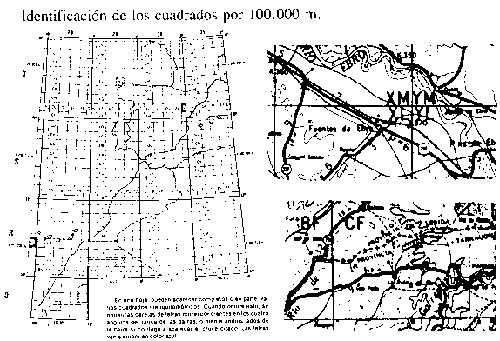

| Cartografía nacional |
Las más extendidas son la escala 1:200.000 (aproximadamente un rectángulo de dimensiones 80 km x 40 km), la escala 1:100.000 (aproximadamente 40 km x 20 km) y la escala 1:50.000.(aproximadamente 20 km x 10 km)
Todos los mapas tienen 2 tipos de notación para su localización:
Un nombre que hace referencia a una ciudad o población importante que se encuentre dentro de la hoja topográfica. Por ejemplo: Madrid, Liria, Algete, etc. Y una pareja de números separados por un guión. Estos números hacen referencia a una serie de columnas y filas determinadas arbitrariamente en la Península Ibérica, Islas Baleares e Islaas Canarias. El primer número hace referencia a la numeración de las columnas, que aumenta de Oeste a Este; y el segundo hace referencia a la numeración de las filas, que aumenta de Norte a Sur. Esta notación es válida para varias escalas.
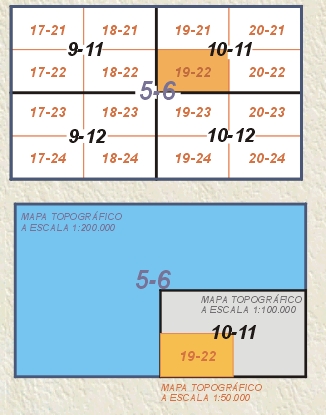 |
En este ejemplo se muestra donde está localizado el mapa topográfico a escala 1:50.000 correspondiente a la ciudad de Madrid (mapa 19-22, escala 1:50.000). |
Existe otra notación utilizada para los mapas a escala 1:50.000, y es una numeración de los mapas existentes, consecutiva de Oeste a Este y de Norte a Sur. Por ejemplo, el mapa a escala 1:50.000 de la ciudad de Madrid, es el mapa número 559 (19-22)
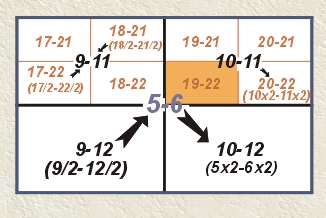
Para poder situar rápidamente un mapa a una escala determinada en otro de escala mayor o menor, basta con realizar un pequeña operación.
Para conocer el numero de la hoja de escala inmediata inferior (denominador mayor) que comprenda a una dada, bastará dividir por dos cada uno de sus números, tomando los cocientes por exceso cuando no sean enteros. Por ejemplo: queremos saber en que mapa a escala 1:100.000 se encuentra el mapa 17-22 (a escala 1:50.000), debemos dividir 17 y 22 entre 2, lo que resulta 8,5 y 11, como 8,5 es un número no entero tomamos el siguiente es decir el 9. Por lo tanto el mapa que buscamos es el 9-11 (escala 1:100.000).
Para conocer el numero de la hoja de escala inmediata superior (denominador menor) que comprenda a una dada, bastará con multiplicar ambos números por 2, obteniéndose el número de la hoja de la esquina inferior izquierda (cuadrante SE). Por ejemplo queremos saber a que mapas a escala 1:50.000 corresponde el mapa 10-11 (a escala 1:100.000), multiplicamos ambos números (10 y 11) por 2 y obtenemos 20-22, este mapa será el del cuadrantes SE de los cuatro mapas a escala 1:50.000 que componen el mapa 10-11 (escala 1:100.000).
 |
El Instituto Geográfico Nacional de España, publica también una serie de mapas a escala 1:25.000. Estos mapas tienen otra notación diferente. Van precedidos de un número en caracteres arábigos seguido de otro número (del 1 al 4) en números romanos. El primer número corresponde al mapa escala 1:50.000 en el que están englobados esos mapas (559, aunque también puede aparecer con la notación de los dos números separados por un guión, p. ej. 19-22). el número romano a continuación hace referencia al cuadrante de mapa: I cuadrante NO; II cuadrante NE, III cuadrante SO y IV cuadrante SE. |
| Calcular el QTH locator |
El locator se utiliza por los radioaficionados para expresar la situación exacta desde donde se transmite.
El mundo se divide en 324 grandes áreas, estas áreas cubren 10 grados de Latitud por 20 grados de Longitud, a lo cual se les llama Campos.
Básicamente está compuesto por una combinación de seis dígitos de números y letras (dos letras-dos números-dos letras); los dígitos 1º, 3º y 5º se refieren a la longitud, y los dígitos 2º, 4º y 6º se refieren a la latitud.
En este caso el Campo serían las DOS primeras cifras, que en España son las correspondientes a IN, JN, IM e IL.
El Campo tiene:
Cada Campo a su vez se divide en 100 Cuadrículas. Cada una de esas 100 Cuadrículas representan 1 grado en la Latitud por 2 grados en la Longitud, es decir, 60 x 120 Millas Náuticas. Estas confoman las cuatro primeras cifras del locator (IL68).
Existen dos cifras más, que en este caso serían las letras JV, (IL68JV); estas dos últimas letras, definen la localización con mayor exactitud, dividiendo ese campo y cuadrícula IL68, en una sub-cuadrícula. Esta Sub-Cuadrícula se divide a su vez en 5 minutos por 2.5 minutos. (Recuerden que un minuto de la Latitud es igual a 1 Milla Náutica).
La Subcuadrícula tiene:
Por lo tanto, para calcular el Locator, es preciso conocer previamente la coordenadas geográficas de nuestra ubicación en grados y minutos; se puede obtener de un mapa geográfico de la zona o de un receptor GPS. Debemos seguir los siguientes pasos:
1. Tomamos la longitud y convertimos los grados sexagesimales en grados centesimales.
2. Si te encuentras al Este del meridiano de Greenwich, suma 180 a la cifra anterior.
3. Si te encuentras al Oeste del meridiano de Greenwich, resta 180 a la cifra anterior.
4. Divide el resultado entre dos.
5. Divide el valor obtenido por diez y anota las cifras situadas a la izquierda del punto decimal,se obtiene así el primer dígito (ver tabla 1).
6. Multiplica por diez la cifra anterior y anota la primera cifra situada inmediatamente a la izquierda del punto decimal, se obtendrá el tercer dígito.
7. Toma los decimales de la cifra anterior y multiplícalos por 24. Con las cifras situadas a la izquierda del punto decimal se obtiene el quinto dígito (ver tabla 1).
8. Tomamos la latitud y convertimos los grados sexagesimales en grados centesimales.
9. Si te encuentras al Norte del Ecuador, suma 90 a la cifra anterior.
10. Si te encuentras al Sur del Ecuador, réstale 90 a la cifra anterior.
11. Divide el resultado por diez y anota las cifras situadas a la izquierda del punto decimal para obtener el segundo dígito (ver tabla 1).
12. Multiplica por diez y anota el numero situado inmediatamente a la izquierda del punto decimal, este será el cuarto dígito.
13. Toma los decimales del valor obtenido y multiplícalos por 24. Las cifras situadas a la izquierda del punto decimal nos dan el sexto dígito (ver tabla 1).
| 0 = A | 4 = E | 8 = I | 12 = M | 16 = Q | 20 = U |
| 1 = B | 5 = F | 9 = J | 13 = N | 17 = R | 21 = V |
| 2 = C | 6 = G | 10 = K | 14 = O | 18 = S | 22 = W |
| 3 = D | 7 = H | 11 = L | 15 = P | 19 = T | 23 = X |
Ejemplo:
Supongamos que nos encontramos en un punto geográfico cuyas coordenadas son, 7º 8´ Oeste y 28º 54´ Norte (Halum).
Pasamos la longitud a grados centesimales (7º 8´ = 7'13), restamos 180 (7'13 - 180 = -172'87), dividimos entre 2 (172'87 / 2 = 86'43), dividimos el valor entre diez (86'43 / 10 = 8'64), tomamos las cifras situadas a la izquierda del punto decimal y consultamos la tabla 1 para obtener el primer dígito(8 = I), multiplicamos por diez (8'64 X 10 = 86'4), anotamos la primera cifra situada inmediatamente a la izquierda del punto decimal para obtener el tercer dígito (6), tomamos los decimales del valor obtenido y multiplicamos por 24 (0'4 X 24 = 9'6), tomamos las cifras situadas a la izquierda del punto decimal para obtener el quinto dígito (9 = J).
Pasamos la latitud a grados centesimales (28º 54´ = 28'9), sumamos 90 (28'9 + 90 = 118'9),dividimos entre diez (118'9 / 10 = 11'89), anotamos las cifras situadas a la izquierda del punto decimal y consultamos la tabla 1 para obtener el segundo dígito (11 = L), multiplicamos por diez (11'89 X 10 = 118'9), anotamos la primera cifra situada inmediatamente a la izquierda del punto decimal para obtener el cuarto dígito (8), tomamos los decimales del valor obtenido y multiplicamos por 24 (0'9 X 24 = 21'6), por ultimo tomamos las cifras situadas a la izquierda del punto decimal y consultamos la tabla 1 para obtener el sexto dígito (21 = V).
Por tanto el locator de Halum es : IL68JV
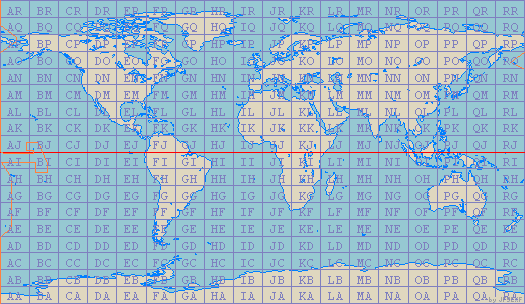
| Conversor de coordenadas |
|
De grados en decimal a grados, minutos y segundos
|
| Datos geográficos del mundo |
| Constantes de la Tierra |
Volumen |
1.083.207.320.000 km3 |
Masa |
5.974.222 x 1015 t. |
Area |
510.065.622 km2 |
Superficie de tierra |
149.4 x 106 km2 (29.22%) |
Radio Ecuatorial |
6378.14 km |
Radio Polar |
6356.75 km |
Radio medio |
6371 km |
Longitud de la circunferencia Ecuatorial |
40075.2 km |
Longitud de la circunferencia meridional |
40008.1 km |
Superficie de agua |
360.6 x 106 km2 (70.78%) |
Altitud máxima en el continente |
8848 metros |
Altitud media en el continente |
840 metros |
Profundidad máxima en los océanos |
11035 metros |
Profundidad media en los océanos |
3808 metros |
| Extremos terrestres |
Lugar más lluvioso |
Monte Waialeale (Hawai). Media anual: 1.196 cm (en 1981, récord en un año en Arenapunji, 2.646 cm). |
Lugar más seco |
Desierto de Atacama (Chile). Precipitación inapreciable en Atacama no se ha registrado ninguna lluvia. |
Lugar más caluroso |
Al'Aziziyah (Arabia Saudí), 57ºC registrados en 1922. |
Lugar más frío |
Vostok (Antártida), -88ºC registrados en 1960. |
Ciudad más al Norte |
Ny Alesund (Spitzbergen). |
Ciudad más al Sur |
Puerto Williams (Chile). |
Ciudad más alta |
Aucanquilcha (Chile): 5.334 m. |
Ciudad más baja |
Publos en el mar Muerto: -392 m. |
Mayor barranco |
Gran Cañón - Río Colorado (Arizona - USA): 349 km de longitud, 6 a 21 km de ancho y 1.6 km de profundidad. |
Barranco más profundo |
Cañón de Hells - Río Snake (Idaho - USA): 20.47 m. |
Viento más fuerte |
Monte Washington - New Hampshire: 371 km/h registrado en 1934. |
Mayor marea |
Bahía de Fundy - Nueva Escocia: 16 m. |
Mayor cráter meteórico |
Cráter de Chubb (Canadá): 3 km de ancho. |
| Océanos |
Nombre |
Área (km2) |
% del agua terrestre |
Mayor profundidad (m) |
|---|---|---|---|
Pacífico |
165.235.200 |
45.8 |
Fosa de Filipinas (11.516) |
Atlántico |
82.436.300 |
22.8 |
Fosa de Puerto Rico (8.381) |
Índico |
73.449.400 |
20.6 |
Profundidad Diamantina (8.047) |
Ártico |
14.089.000 |
3.9 |
Sin nombre (5.450) |
Antártico |
8.000.000 |
2.2 |
|
| Mares más importantes |
Nombre |
Área (km2) |
Profundidad media (m) |
|---|---|---|
Mar Caribe |
2.754.050 |
2.491 |
Mar Mediterráneo |
2.503.900 |
1.487 |
Mar de Bering |
2.268.200 |
1.437 |
Golfo de México |
1.543.018 |
1.512 |
Mar de Okhotsk |
1.527.600 |
838 |
Mar del Este de China |
1.249.201 |
188 |
Bahía de Hudson |
1.232.301 |
128 |
Mar del Japón |
1.007.701 |
1.350 |
Mar de Andamán |
797.601 |
870 |
Mar del Norte |
575.301 |
94 |
Mar Negro |
461.999 |
1.110 |
Mar Rojo |
437.899 |
491 |
Mar Báltico |
422.300 |
58 |
| Lagos más importantes |
Nombre |
Área (km2) |
Mayor profundidad (m) |
Mar Caspio (Europa-Asia) |
371.794 |
980 |
Superior (USA-Canadá) |
82.414 |
406 |
Victoria (Africa) |
69.484 |
81 |
Mar de Aral (Uzbekistán-Kazajstán) |
65.527 |
68 |
Huron (USA-Canadá) |
59.596 |
229 |
Michigan (USA) |
58.016 |
281 |
Tanganika (Africa) |
32.893 |
1.435 |
Lago del Oso (Canadá) |
31.792 |
137 |
Baikal (Federación Rusa) |
30.510 |
1.620 |
Nyasa (Africa) |
29.604 |
678 |
| Islas más importantes |
Nombre |
Superficie (km2) |
Mar |
País |
Groenlandia |
2.175.600 |
Artico |
Dinamarca |
Nueva Guinea |
821.030 |
Pacífico |
Indonesia-Papua |
Borneo |
744.366 |
Indico |
Indonesia-Malasia-Brunei |
Madagascar |
595.213 |
Indico |
Madagascar |
Baffin |
476.068 |
Artico |
Canadá |
Sumatra |
473.607 |
Indico |
Indonesia |
Honshu u Hondo |
227.920 |
Pacífico |
Japón |
Gran Bretaña |
218.042 |
Atlántico |
Gran Bretaña |
Ellesmere |
212.688 |
Artico |
Canadá |
Victoria |
212.199 |
Artico |
Canadá |
| Ríos de mayor longitud |
Nombre |
Longitud (km) |
Nilo-Kagera (Africa) |
6.669 |
Amazonas (América del Sur) |
6.437 |
Yangtze (China) |
6.380 |
Mississippi-Missouri (USA) |
5.970 |
Obi-Irtish (Federación Rusa) |
5.567 |
Huang (China) |
4.827 |
Congo o Zaire (Africa) |
4.667 |
Paraná (América del Sur) |
4.500 |
Mekong (Asia) |
4.500 |
Amur (Asia) |
4.416 |
Lena (Federación Rusa) |
4.312 |
Mackenzie-Peace (Canadá) |
4.240 |
Niger (Africa) |
4.183 |
Yenisey (Siberia) |
4.129 |
Murray-Darling (Australia) |
3.716 |
Volga (Federación Rusa) |
3.684 |
| Grandes desiertos |
Nombre |
Superficie (km2) |
|---|---|
Sáhara (Norte de Africa) |
9.100.000 |
Libia (Norte de Africa) |
1.680.000 |
Australiano (Australia) |
1.550.000 |
Arábigo (Arabia) |
1.300.000 |
Gobi (Mongolia) |
1.040.000 |
Rub'al-Khali (Arabia) |
647.500 |
Kalahari (Botswana - Africa) |
520.000 |
Sirio (Norte de Arabia) |
310.000 |
Takla-Makan (Sinkiang (China) - Asia) |
310.000 |
Karakumy (Turkmenistán) |
260.000 |
Nubia (Este del Sáhara - Africa) |
260.000 |
Thar (NO. de India y E. de Pakistán - Asia) |
250.000 |
Kyzyl Kum (Uzbekistán-Kazajstán) |
225.000 |
| Cordilleras más altas y sus cimas |
Cordillera |
Cima |
País |
Continente |
Altitud (m) |
Himalaya |
Everest |
Nepal-Tibet |
Asía |
8.844,43 |
Karakorum |
K2 |
Cachemira |
Asía |
8.611 |
Kunlún Shan |
Muztag |
China |
Asía |
7.723 |
Hindu Kush |
Tirich Mir |
Pakistán |
Asía |
7.690 |
Tahsueh Shan |
Minya Konka |
China |
Asía |
7.590 |
Pamir |
Kommunizma |
Tadyikistán |
Asía |
7.495 |
Amne Machin |
Amne Machin |
China |
Asía |
7.160 |
Kailas |
Lombo Kangra |
Tibet |
Asía |
7.061 |
Andes |
Aconcagua |
Argentina |
América del Sur |
6.960 |
Salto-Jujeña |
Cerro Galán |
Argentina |
América del Sur |
6.600 |
S. Pampeanas |
Manuel Belgrano |
Argentina |
América del Sur |
6.250 |
Alaska |
Mckinley |
USA |
América del Norte |
6.194 |
San Elías |
Logan |
Canadá |
América del Norte |
6.050 |
Pare |
Kilimanjaro |
Tanzania |
Africa |
5.895 |
Santa Marta |
Cristóbal Colón |
Colombia |
América del Sur |
5.775 |
Cáucaso |
El'Brus |
Federación Rusa |
Europa |
5.642 |
Alpes |
Mont blanc |
Francia |
Europa |
4.807 |
Teide |
Teide |
España |
Europa |
3.718 |
Sierra Nevada |
Mulhacén |
España |
Europa |
3.481 |
Pirineos |
Pico de Aneto |
España |
Europa |
3.478 |
| Datos geográficos de España |
Latitud y Longitud de los puntos extremos de España y altitudes máximas.
| Localización geográfica |
| Península | Latitud Norte | Extremo septentrional | Punta La Estaca de Bares (La Coruña) | 43º 47' 33" |
| Extremo meridional | Isleta de Tarifa (Cádiz) | 36º 00' 03" | ||
| Longitud | Extremo oriental | Cap de Creus (Girona) | 03º 19' 15" E | |
| Extremo occidental | Cabo Touriñan (La Coruña) | 09º 17' 56" O | ||
| Altitud máxima | Pico de Mulhacén | Sierra Nevada (Granada) | 3.478 m sobre el nivel del mar | |
| Illes Balears | Latitud Norte | Extremo septentrional | Isla de Santija o des Porros | 40º 05' 37" |
| Extremo meridional | Cap de Barbaria (Isla de Formentera) | 38º 38' 25" | ||
| Longitud | Extremo oriental | Punta de s'Esperó (Isla de Menorca) | 04º 19' 35" E | |
| Extremo occidental | Es Vedrà | 01º 12' 12" E | ||
| Altitud máxima | Puig Major | (Isla de Mallorca) | 1.445 m sobre el nivel del mar | |
| Islas Canarias | Latitud Norte | Extremo septentrional | Punta Mosegos (Isla de Alegranza) | 29º 24' 35" |
| Extremo meridional | Punta de los Saltos (Isla de Hierro) | 27º 38' 12" | ||
| Longitud | Extremo oriental | Roque del Este (Isla de Lanzarote) | 13º 19' 57" O | |
| Extremo occidental | Punta Orchilla (Isla de Hierro) | 18º 09' 36" O | ||
| Altitud máxima | Teide | (Isla de Tenerife) | 3.178 m sobre el nivel del mar | |
| Ciudades del Norte de Africa | Latitud Norte | Extremo septentrional | Ceuta | 35º 55' 05" |
| Extremo meridional | Peñón de Vélez de la Gomera | 35º 10' 24" | ||
| Longitud | Extremo oriental | Isla del Rey (Chafarinas) | 02º 24' 55" O | |
| Extremo occidental | Ceuta | 05º 22' 56" O | ||
| Altitud máxima | Ceuta | 345 m sobre el nivel del mar |
| Altitudes máxima y mínima de las provincias |
| Alava | Peña Gorbea | 1475 m | Río Ebro | 376 m |
| Albacete | Almenaras | 1797 m | Río Segura | 310 m |
| Alicante | Aitana | 1558 m | Nivel del mar | |
| Almería | Chullo | 2606 m | Nivel del mar | |
| Asturias | Torre de Cerredo | 2648 m | Nivel del mar | |
| Avila | Almanzor | 2591 m | Río Tiétar | 295 m |
| Badajoz | Tentudía | 1110 m | Río Guadiana | 110 m |
| Balears, Illes | Puig Major | 1145 m | Nivel del mar | |
| Barcelona | Tossa | 2531 m | Nivel del mar | |
| Burgos | San Millán | 2131 m | Río Ebro | 450 m |
| Cáceres | Calvitero | 2425 m | Río Tajo | 70 m |
| Cádiz | Pinar | 1654 | Nivel del mar | |
| Cantabria | Peña Vieja | 2613 m | Nivel del mar | |
| Castellón | Peñagolosa | 1813 m | Nivel del mar | |
| Ciudad Real | Amor | 1371 m | Río Guadiana | 360 m |
| Córdoba | Horconera | 1570 m | Río Guadalquivir | 35 m |
| Coruña, La | Coba da Serpe | 898 | Nivel del mar | |
| Cuenca | San Felipe | 1839 m | Río Cabriel | 480 m |
| Girona | Puigmale | 2913 m | Nivel del mar | |
| Granada | Mulhacén | 3478 m | Nivel del mar | |
| Guadalajara | Lobo | 2262 m | Río Tajo | 570 m |
| Guipúzcoa | Aitzgorri | 1544 m | Nivel del mar | |
| Huelva | Almonaster | 912 m | Nivel del mar | |
| Huesca | Aneto | 3404 m | Río Segre | 70 m |
| Jaén | Sierra Mágina | 2167 m | Río Guadalquivir | 150 m |
| León | Torre de Cerredo | 2648 m | Río Esla | 710 m |
| Lleida | Coma Pedrosa | 3115 m | Río Ebro | 65 m |
| Rioja, La | San Lorenzo | 2262 m | Río Ebro | 260 m |
| Lugo | Peña Rubia | 1821 m | Nivel del mar | |
| Madrid | Peñalara | 2430 m | Río Tajo | 470 m |
| Málaga | Maroma | 2065 m | Nivel del mar | |
| Murcia | Revolcadores | 2001 m | Nivel del mar | |
| Navarra | Mesa de los Tres Reyes | 2433 m | Río Ebro | 235 m |
| Ourense | Peña Trevinca | 2095 m | Río Miño | 40 m |
| Palencia | Peña Prieta | 2536 m | Río Pisuerga | 695 m |
| Palmas, Las | Pico de las Nieves | 1949 m | Nivel del mar | |
| Pontevedra | Faro de Chantada | 1177 m | Nivel del mar | |
| Salamanca | Calvitero | 2425 m | Río Duero | 130 m |
| Santa Cruz de Tenerife | Teide | 3718 m | Nivel del mar | |
| Segovia | Peñalara | 2430 m | Río Eresma | 735 m |
| Sevilla | Terril | 1129 m | Nivel del mar | |
| Soria | Moncayo | 2313 m | Río Jalón | 750 m |
| Tarragona | Monte Caro | 1447 m | Nivel del mar | |
| Teruel | Peñarroya | 2024 m | Río Martín | 140 m |
| Toledo | Rocigalgo | 1447 m | Río Tajo | 290 m |
| Valencia | Palomeras | 1258 m | Nivel del mar | |
| Valladolid | Sardanedo | 854 m | Río Duero | 645 |
| Vizcaya | Peña Gorbea | 1475 m | Nivel del mar | |
| Zamora | Peña Negra | 2124 m | Río Duero | 335 m |
| Zaragoza | Moncayo | 2313 m | Río Ebro | 65 m |
| Ceuta | 345 m | Nivel del mar | ||
| Melilla | Nivel del mar |
| Principales cumbres montañosas |
Nombre |
Sistema orográfico |
Altitud (m) |
|---|---|---|
Teide (Tenerife) |
Islas Canarias |
3.718 |
Mulhacén (Granada) |
Serranias Penibeticas |
3.478 |
Aneto (Huesca) |
Cordillera Pirenaica |
3.404 |
Pico del Veleta (Granada) |
Serranias Penibeticas |
3.392 |
Les Posets o Lardana (Huesca) |
Cordillera Pirenaica |
3.375 |
Alcazaba (Granada) |
Serranias Penibeticas |
3.366 |
Monte Perdido (Huesca) |
Cordillera Pirenaica |
3.355 |
Cilindro (Huesca) |
Cordillera Pirenaica |
3.328 |
Perdiguero (Huesca) |
Cordillera Pirenaica |
3.321 |
La Maladeta (Huesca) |
Cordillera Pirenaica |
3.309 |
| Ríos principales |
Nombre |
Longitud (km) |
Afluentes |
|
Margen derecha |
Margen izquierda |
||
Tajo |
1.007 |
Cabrillas (45) |
Arroyo Solana (26) |
Ebro |
910 |
Jerea (45) |
Aragón (197) |
Duero |
895 |
Ebrillos (32) |
Tera (33) |
Guadalquivir |
657 |
Guadalimar (167) |
Guadiana Menor (94) |
Guadiana |
578 |
Bullaque (86) |
Azuer (89) |
Júcar |
498 |
Canal de Maria Cristina 124) |
|
Genil (Guadalquivir) |
337 |
|
|
Segura |
325 |
Tus (40) |
|
Miño |
310 |
Parga (30) |
Neira (55) |
Turia |
280 |
|
|
Pisuerga (Duero) |
275 |
|
|
Esla (Duero) |
275 |
|
|
| Costas españolas |
Provincia |
Longitud (km) |
Provincia |
Longitud (km) |
|---|---|---|---|
Girona |
257 |
Pontevedra |
388 |
Barcelona |
166 |
A Coruña |
944 |
Tarragona |
277 |
Lugo |
129 |
Castellón |
139 |
Asturias |
412 |
Valencia |
135 |
Cantabria |
279 |
Alicante |
252 |
Vizcaya |
153 |
Alicante |
252 |
Guipúzcoa |
89 |
Murcia |
269 |
Baleares |
1.283 |
Almería |
248 |
Melilla |
12 |
Granada |
78 |
Ceuta |
26 |
Málaga |
179 |
Las Palmas |
799 |
Cádiz |
447 |
Santa Cruz de Tenerife |
702 |
Huelva |
122 |
TOTAL |
7.785 |
| Altura sobre el nivel del mar de ciudades españolas |
Provincia |
Altitud en m |
Provincia |
Altitud en m |
|---|---|---|---|
A Coruña |
26 |
Lugo |
454 |
Albacete |
686 |
Madrid |
655 |
Alicante |
8 |
Málaga |
11 |
Almeria |
16 |
Melilla |
40 |
Avila |
1131 |
Murcia |
39 |
Badajoz |
186 |
Ourense |
139 |
Barcelona |
12 |
Oviedo (Asturias) |
228 |
Bilbao (Vizcaya) |
6 |
Palencia |
734 |
Burgos |
929 |
Palma de Mallorca (I. Balears) |
15 |
Cáceres |
459 |
Pamplona (Navarra) |
490 |
Cádiz |
69 |
Pontevedra |
27 |
Castellón de la Plana |
27 |
Salamanca |
800 |
Ceuta |
30 |
San Sebastian (Guipuzcoa) |
5 |
Ciudad Real |
628 |
Santa Cruz de Tenerife |
4 |
Córdoba |
123 |
Santander (Cantabria) |
11 |
Cuenca |
999 |
Segovia |
1002 |
Girona |
70 |
Sevilla |
11 |
Granada |
685 |
Soria |
1063 |
Guadalajara |
685 |
Tarragona |
22 |
Huelva |
30 |
Teruel |
917 |
Huesca |
488 |
Toledo |
529 |
Jaén |
568 |
Valencia |
13 |
Las Palmas de Gran Canaria |
13 |
Valladolid |
698 |
León |
838 |
Vitoria (Alava) |
540 |
Lleida |
182 |
Zamora |
649 |
Logroño (La Rioja) |
384 |
Zaragoza |
199 |
| Distancia aproximada por carretera entre capitales de provincia |
|
| Albacete | Alicante | Almería | Ávila | Badajoz | Barcelona | |
| Albacete | 0 | 170 | 369 | 367 | 525 | 540 |
| Alicante | 171 | 0 | 294 | 538 | 696 | 515 |
| Almería | 369 | 294 | 0 | 664 | 604 | 809 |
| Ávila | 367 | 538 | 664 | 0 | 318 | 717 |
| Badajoz | 525 | 696 | 604 | 318 | 0 | 1022 |
| Barcelona | 540 | 515 | 809 | 717 | 1022 | 0 |
| Bilbao | 646 | 817 | 958 | 401 | 694 | 620 |
| Burgos | 487 | 658 | 801 | 244 | 537 | 582 |
| Cáceres | 504 | 675 | 651 | 229 | 89 | 918 |
| Cádiz | 617 | 688 | 484 | 618 | 342 | 1284 |
| Castellón | 256 | 231 | 525 | 532 | 805 | 284 |
| Ciudad Real | 208 | 377 | 408 | 257 | 317 | 812 |
| Córdoba | 354 | 525 | 332 | 457 | 372 | 908 |
| Cuenca | 142 | 313 | 511 | 282 | 555 | 562 |
| Gerona | 641 | 614 | 910 | 818 | 1123 | 101 |
| Granada | 363 | 353 | 166 | 534 | 438 | 868 |
| Guadalajara | 309 | 480 | 621 | 173 | 459 | 563 |
| Huelva | 506 | 703 | 516 | 552 | 251 | 1140 |
| Huesca | 496 | 570 | 829 | 491 | 797 | 275 |
| Jaén | 264 | 415 | 228 | 435 | 376 | 804 |
| La Coruña | 860 | 1031 | 1172 | 538 | 772 | 1118 |
| León | 584 | 755 | 896 | 255 | 496 | 784 |
| Lérida | 515 | 490 | 802 | 558 | 866 | 156 |
| Logroño | 579 | 654 | 898 | 359 | 677 | 468 |
| Lugo | 762 | 933 | 1074 | 440 | 674 | 1020 |
| Madrid | 251 | 422 | 563 | 115 | 401 | 621 |
| Málaga | 473 | 482 | 219 | 644 | 436 | 997 |
| Murcia | 149 | 76 | 218 | 516 | 675 | 590 |
| Orense | 772 | 943 | 1084 | 443 | 645 | 1027 |
| Oviedo | 702 | 873 | 1014 | 373 | 614 | 902 |
| Palencia | 491 | 662 | 803 | 168 | 461 | 669 |
| Pamplona | 597 | 674 | 971 | 438 | 756 | 438 |
| Pontevedra | 874 | 1045 | 1186 | 545 | 747 | 1129 |
| Salamanca | 463 | 634 | 763 | 97 | 299 | 778 |
| San Sebastián | 691 | 766 | 1032 | 475 | 768 | 527 |
| Santander | 645 | 816 | 957 | 368 | 663 | 694 |
| Segovia | 338 | 509 | 650 | 67 | 385 | 650 |
| Sevilla | 492 | 609 | 422 | 493 | 217 | 1046 |
| Soria | 473 | 548 | 794 | 261 | 579 | 453 |
| Tarragona | 442 | 418 | 712 | 648 | 936 | 99 |
| Teruel | 242 | 317 | 577 | 417 | 703 | 409 |
| Toledo | 240 | 411 | 526 | 137 | 368 | 692 |
| Valencia | 191 | 166 | 460 | 467 | 716 | 349 |
| Valladolid | 445 | 616 | 757 | 122 | 415 | 664 |
| Vitoria | 602 | 739 | 914 | 357 | 650 | 530 |
| Zamora | 499 | 670 | 811 | 159 | 361 | 759 |
| Zaragoza | 423 | 498 | 758 | 418 | 726 | 296 |
| Albacete | Alicante | Almería | Ávila | Badajoz | Barcelona |
| Bilbao | Burgos | Cáceres | Cádiz | Castellón | Ciudad Real | |
| Albacete | 646 | 487 | 504 | 617 | 256 | 208 |
| Alicante | 817 | 658 | 675 | 688 | 231 | 377 |
| Almería | 958 | 801 | 651 | 484 | 525 | 408 |
| Ávila | 401 | 244 | 229 | 618 | 532 | 257 |
| Badajoz | 694 | 537 | 89 | 342 | 805 | 317 |
| Barcelona | 620 | 582 | 918 | 1284 | 284 | 812 |
| Bilbao | 0 | 159 | 605 | 1058 | 607 | 586 |
| Burgos | 159 | 0 | 447 | 900 | 524 | 428 |
| Cáceres | 605 | 447 | 0 | 389 | 701 | 325 |
| Cádiz | 1058 | 900 | 389 | 0 | 873 | 465 |
| Castellón | 607 | 524 | 701 | 873 | 0 | 462 |
| Ciudad Real | 586 | 428 | 325 | 465 | 462 | 0 |
| Córdoba | 795 | 637 | 319 | 263 | 610 | 201 |
| Cuenca | 562 | 404 | 451 | 708 | 305 | 244 |
| Gerona | 719 | 984 | 1018 | 1385 | 383 | 912 |
| Granada | 829 | 671 | 485 | 335 | 584 | 278 |
| Guadalajara | 396 | 238 | 355 | 721 | 396 | 248 |
| Huelva | 939 | 781 | 323 | 219 | 856 | 433 |
| Huesca | 323 | 358 | 695 | 1061 | 356 | 588 |
| Jaén | 730 | 572 | 423 | 367 | 520 | 179 |
| La Coruña | 644 | 535 | 683 | 1072 | 1026 | 799 |
| León | 359 | 201 | 407 | 796 | 725 | 511 |
| Lérida | 464 | 427 | 762 | 1128 | 259 | 655 |
| Logroño | 153 | 114 | 596 | 998 | 455 | 525 |
| Lugo | 546 | 437 | 585 | 974 | 928 | 696 |
| Madrid | 395 | 237 | 297 | 663 | 417 | 190 |
| Málaga | 939 | 781 | 506 | 265 | 713 | 388 |
| Murcia | 796 | 638 | 654 | 613 | 306 | 357 |
| Orense | 605 | 447 | 556 | 945 | 938 | 699 |
| Oviedo | 304 | 322 | 525 | 914 | 868 | 641 |
| Palencia | 244 | 86 | 372 | 761 | 596 | 424 |
| Pamplona | 158 | 204 | 651 | 1071 | 457 | 598 |
| Pontevedra | 707 | 549 | 658 | 1047 | 1040 | 701 |
| Salamanca | 395 | 237 | 210 | 599 | 629 | 353 |
| San Sebastián | 119 | 232 | 679 | 1132 | 551 | 659 |
| Santander | 107 | 157 | 574 | 1057 | 681 | 584 |
| Segovia | 355 | 197 | 296 | 750 | 504 | 277 |
| Sevilla | 933 | 775 | 264 | 125 | 762 | 339 |
| Soria | 257 | 141 | 490 | 894 | 383 | 421 |
| Tarragona | 556 | 519 | 832 | 1060 | 187 | 648 |
| Teruel | 488 | 372 | 599 | 873 | 152 | 397 |
| Toledo | 466 | 308 | 264 | 583 | 437 | 119 |
| Valencia | 633 | 517 | 636 | 808 | 65 | 398 |
| Valladolid | 281 | 123 | 326 | 715 | 564 | 378 |
| Vitoria | 66 | 114 | 561 | 1014 | 574 | 541 |
| Zamora | 376 | 218 | 272 | 661 | 665 | 415 |
| Zaragoza | 324 | 287 | 622 | 988 | 283 | 515 |
| Bilbao | Burgos | Cáceres | Cádiz | Castellón | Ciudad Real |
| Córdoba | Cuenca | Gerona | Granada | Guadalajara | Huelva | |
| Albacete | 354 | 142 | 641 | 363 | 309 | 506 |
| Alicante | 525 | 313 | 614 | 353 | 480 | 703 |
| Almería | 332 | 511 | 910 | 166 | 621 | 516 |
| Ávila | 457 | 282 | 818 | 534 | 173 | 552 |
| Badajoz | 372 | 555 | 1123 | 438 | 459 | 251 |
| Barcelona | 908 | 562 | 101 | 868 | 563 | 1140 |
| Bilbao | 795 | 562 | 719 | 829 | 396 | 939 |
| Burgos | 637 | 404 | 984 | 671 | 238 | 781 |
| Cáceres | 319 | 451 | 1018 | 485 | 355 | 323 |
| Cádiz | 263 | 708 | 1385 | 335 | 721 | 219 |
| Castellón | 610 | 305 | 383 | 584 | 396 | 856 |
| Ciudad Real | 201 | 244 | 912 | 278 | 248 | 433 |
| Córdoba | 0 | 445 | 1009 | 166 | 458 | 232 |
| Cuenca | 445 | 0 | 661 | 479 | 186 | 677 |
| Gerona | 1009 | 661 | 0 | 968 | 663 | 1240 |
| Granada | 166 | 479 | 968 | 0 | 492 | 350 |
| Guadalajara | 458 | 186 | 663 | 492 | 0 | 690 |
| Huelva | 232 | 677 | 1240 | 350 | 690 | 0 |
| Huesca | 798 | 405 | 375 | 832 | 338 | 1028 |
| Jaén | 104 | 380 | 904 | 99 | 393 | 336 |
| La Coruña | 995 | 776 | 1217 | 1043 | 667 | 1006 |
| León | 733 | 500 | 884 | 761 | 391 | 730 |
| Lérida | 865 | 472 | 256 | 861 | 407 | 1097 |
| Logroño | 736 | 464 | 568 | 772 | 278 | 968 |
| Lugo | 897 | 678 | 1120 | 945 | 569 | 908 |
| Madrid | 400 | 167 | 721 | 434 | 58 | 632 |
| Málaga | 187 | 615 | 1097 | 129 | 602 | 313 |
| Murcia | 444 | 292 | 690 | 278 | 459 | 628 |
| Orense | 921 | 689 | 1127 | 955 | 579 | 879 |
| Oviedo | 851 | 618 | 1002 | 885 | 509 | 821 |
| Palencia | 640 | 407 | 769 | 674 | 298 | 695 |
| Pamplona | 806 | 536 | 538 | 842 | 348 | 1038 |
| Pontevedra | 977 | 791 | 1229 | 1057 | 681 | 981 |
| Salamanca | 529 | 379 | 878 | 631 | 270 | 533 |
| San Sebastián | 869 | 636 | 629 | 903 | 441 | 1101 |
| Santander | 794 | 561 | 794 | 828 | 395 | 963 |
| Segovia | 497 | 254 | 750 | 521 | 145 | 619 |
| Sevilla | 138 | 583 | 1146 | 256 | 596 | 94 |
| Soria | 631 | 359 | 553 | 665 | 173 | 863 |
| Tarragona | 795 | 463 | 197 | 771 | 475 | 1030 |
| Teruel | 596 | 153 | 509 | 605 | 244 | 842 |
| Toledo | 320 | 187 | 792 | 397 | 129 | 552 |
| Valencia | 545 | 220 | 449 | 519 | 410 | 791 |
| Valladolid | 579 | 361 | 764 | 628 | 252 | 649 |
| Vitoria | 751 | 518 | 630 | 785 | 352 | 919 |
| Zamora | 616 | 415 | 859 | 682 | 306 | 595 |
| Zaragoza | 725 | 334 | 396 | 759 | 267 | 957 |
| Córdoba | Cuenca | Gerona | Granada | Guadalajara | Huelva |
| Huesca | Jaén | La Coruña | León | Lérida | Logroño | |
| Albacete | 496 | 264 | 860 | 584 | 515 | 579 |
| Alicante | 570 | 415 | 1031 | 755 | 490 | 654 |
| Almería | 829 | 228 | 1172 | 896 | 802 | 898 |
| Ávila | 491 | 435 | 538 | 255 | 558 | 359 |
| Badajoz | 797 | 376 | 772 | 496 | 866 | 677 |
| Barcelona | 275 | 804 | 1118 | 784 | 156 | 468 |
| Bilbao | 323 | 730 | 644 | 359 | 464 | 153 |
| Burgos | 358 | 572 | 535 | 201 | 427 | 114 |
| Cáceres | 695 | 423 | 683 | 407 | 762 | 596 |
| Cádiz | 1061 | 367 | 1072 | 796 | 1128 | 998 |
| Castellón | 356 | 520 | 1026 | 725 | 259 | 455 |
| Ciudad Real | 588 | 179 | 799 | 511 | 655 | 525 |
| Córdoba | 798 | 104 | 995 | 733 | 865 | 736 |
| Cuenca | 405 | 380 | 776 | 500 | 472 | 464 |
| Gerona | 375 | 904 | 1217 | 884 | 256 | 568 |
| Granada | 832 | 99 | 1043 | 761 | 861 | 772 |
| Guadalajara | 338 | 393 | 667 | 391 | 407 | 278 |
| Huelva | 1028 | 336 | 1006 | 730 | 1097 | 968 |
| Huesca | 0 | 732 | 904 | 560 | 118 | 244 |
| Jaén | 732 | 0 | 944 | 668 | 779 | 672 |
| La Coruña | 904 | 944 | 0 | 334 | 973 | 649 |
| León | 560 | 668 | 334 | 0 | 628 | 317 |
| Lérida | 118 | 779 | 973 | 628 | 0 | 313 |
| Logroño | 244 | 672 | 649 | 317 | 313 | 0 |
| Lugo | 807 | 846 | 98 | 236 | 875 | 552 |
| Madrid | 397 | 335 | 609 | 333 | 465 | 336 |
| Málaga | 941 | 209 | 1153 | 877 | 1009 | 880 |
| Murcia | 611 | 340 | 1010 | 734 | 583 | 694 |
| Orense | 803 | 856 | 175 | 271 | 871 | 562 |
| Oviedo | 626 | 786 | 340 | 118 | 703 | 391 |
| Palencia | 442 | 575 | 450 | 130 | 513 | 201 |
| Pamplona | 164 | 743 | 739 | 405 | 282 | 89 |
| Pontevedra | 905 | 957 | 121 | 373 | 973 | 664 |
| Salamanca | 554 | 532 | 473 | 197 | 622 | 352 |
| San Sebastián | 255 | 804 | 763 | 433 | 373 | 169 |
| Santander | 431 | 729 | 548 | 294 | 538 | 226 |
| Segovia | 426 | 422 | 560 | 245 | 494 | 299 |
| Sevilla | 935 | 242 | 947 | 671 | 1003 | 874 |
| Soria | 229 | 566 | 676 | 342 | 297 | 105 |
| Tarragona | 210 | 708 | 1065 | 718 | 92 | 402 |
| Teruel | 253 | 506 | 907 | 573 | 319 | 336 |
| Toledo | 468 | 298 | 675 | 392 | 536 | 407 |
| Valencia | 398 | 455 | 961 | 685 | 324 | 481 |
| Valladolid | 438 | 529 | 456 | 135 | 508 | 238 |
| Vitoria | 256 | 686 | 549 | 315 | 374 | 86 |
| Zamora | 535 | 583 | 411 | 135 | 603 | 333 |
| Zaragoza | 72 | 660 | 833 | 488 | 140 | 172 |
| Huesca | Jaén | La Coruña | León | Lérida | Logroño |
| Lugo | Madrid | Málaga | Murcia | Orense | Oviedo | |
| Albacete | 762 | 251 | 473 | 149 | 772 | 702 |
| Alicante | 933 | 422 | 482 | 76 | 943 | 873 |
| Almería | 1074 | 563 | 219 | 218 | 1084 | 1014 |
| Ávila | 440 | 115 | 644 | 516 | 443 | 373 |
| Badajoz | 674 | 401 | 436 | 675 | 645 | 614 |
| Barcelona | 1020 | 621 | 997 | 590 | 1027 | 902 |
| Bilbao | 546 | 395 | 939 | 796 | 605 | 304 |
| Burgos | 437 | 237 | 781 | 638 | 447 | 322 |
| Cáceres | 585 | 297 | 506 | 654 | 556 | 525 |
| Cádiz | 974 | 663 | 265 | 613 | 945 | 914 |
| Castellón | 928 | 417 | 713 | 306 | 938 | 868 |
| Ciudad Real | 696 | 190 | 388 | 357 | 699 | 641 |
| Córdoba | 897 | 400 | 187 | 444 | 921 | 851 |
| Cuenca | 678 | 167 | 615 | 292 | 689 | 618 |
| Gerona | 1120 | 721 | 1097 | 690 | 1127 | 1002 |
| Granada | 945 | 434 | 129 | 278 | 955 | 885 |
| Guadalajara | 569 | 58 | 602 | 459 | 579 | 509 |
| Huelva | 908 | 632 | 313 | 628 | 879 | 821 |
| Huesca | 807 | 397 | 941 | 611 | 803 | 626 |
| Jaén | 846 | 335 | 209 | 340 | 856 | 786 |
| La Coruña | 98 | 609 | 1153 | 1010 | 175 | 340 |
| León | 236 | 333 | 877 | 734 | 271 | 118 |
| Lérida | 875 | 465 | 1009 | 583 | 871 | 703 |
| Logroño | 552 | 336 | 880 | 694 | 562 | 391 |
| Lugo | 0 | 511 | 1055 | 912 | 95 | 242 |
| Madrid | 511 | 0 | 544 | 401 | 521 | 451 |
| Málaga | 1055 | 544 | 0 | 407 | 1065 | 995 |
| Murcia | 912 | 401 | 407 | 0 | 922 | 852 |
| Orense | 95 | 521 | 1065 | 922 | 0 | 337 |
| Oviedo | 242 | 451 | 995 | 852 | 337 | 0 |
| Palencia | 352 | 240 | 784 | 641 | 361 | 248 |
| Pamplona | 641 | 408 | 952 | 715 | 651 | 464 |
| Pontevedra | 148 | 623 | 1153 | 1024 | 102 | 390 |
| Salamanca | 375 | 212 | 756 | 613 | 346 | 315 |
| San Sebastián | 665 | 469 | 1013 | 807 | 679 | 423 |
| Santander | 448 | 394 | 936 | 793 | 545 | 206 |
| Segovia | 462 | 87 | 631 | 488 | 467 | 363 |
| Sevilla | 849 | 538 | 219 | 534 | 820 | 789 |
| Soria | 578 | 231 | 775 | 589 | 574 | 463 |
| Tarragona | 967 | 535 | 898 | 493 | 963 | 836 |
| Teruel | 809 | 302 | 715 | 358 | 805 | 694 |
| Toledo | 577 | 71 | 507 | 390 | 580 | 510 |
| Valencia | 863 | 352 | 648 | 241 | 873 | 803 |
| Valladolid | 356 | 194 | 738 | 595 | 357 | 253 |
| Vitoria | 451 | 351 | 895 | 752 | 561 | 340 |
| Zamora | 313 | 248 | 792 | 649 | 284 | 253 |
| Zaragoza | 735 | 325 | 869 | 539 | 731 | 604 |
| Lugo | Madrid | Málaga | Murcia | Orense | Oviedo |
| Palencia | Pamplona | Pontevedra | Salamanca | San Sebastián | Santander | |
| Albacete | 491 | 597 | 874 | 463 | 691 | 645 |
| Alicante | 662 | 674 | 1045 | 634 | 766 | 816 |
| Almería | 803 | 971 | 1186 | 763 | 1032 | 957 |
| Ávila | 168 | 438 | 545 | 97 | 475 | 368 |
| Badajoz | 461 | 756 | 747 | 299 | 768 | 663 |
| Barcelona | 669 | 438 | 1129 | 778 | 527 | 694 |
| Bilbao | 244 | 158 | 707 | 395 | 119 | 107 |
| Burgos | 86 | 204 | 549 | 237 | 232 | 157 |
| Cáceres | 372 | 651 | 658 | 210 | 679 | 574 |
| Cádiz | 761 | 1071 | 1047 | 599 | 1132 | 1057 |
| Castellón | 596 | 457 | 1040 | 629 | 551 | 681 |
| Ciudad Real | 424 | 598 | 701 | 353 | 659 | 584 |
| Córdoba | 640 | 806 | 977 | 529 | 869 | 794 |
| Cuenca | 407 | 536 | 791 | 379 | 636 | 561 |
| Gerona | 769 | 538 | 1229 | 878 | 629 | 794 |
| Granada | 674 | 842 | 1057 | 631 | 903 | 828 |
| Guadalajara | 298 | 348 | 681 | 270 | 441 | 395 |
| Huelva | 695 | 1038 | 981 | 533 | 1101 | 963 |
| Huesca | 442 | 164 | 905 | 554 | 255 | 431 |
| Jaén | 575 | 743 | 957 | 532 | 804 | 729 |
| La Coruña | 450 | 739 | 121 | 473 | 763 | 548 |
| León | 130 | 405 | 373 | 197 | 433 | 294 |
| Lérida | 513 | 282 | 973 | 622 | 373 | 538 |
| Logroño | 201 | 89 | 664 | 352 | 169 | 226 |
| Lugo | 352 | 641 | 148 | 375 | 665 | 448 |
| Madrid | 240 | 408 | 623 | 212 | 469 | 394 |
| Málaga | 784 | 952 | 1153 | 756 | 1013 | 936 |
| Murcia | 641 | 715 | 1024 | 613 | 807 | 793 |
| Orense | 361 | 651 | 102 | 346 | 679 | 545 |
| Oviedo | 248 | 464 | 390 | 315 | 423 | 206 |
| Palencia | 0 | 288 | 463 | 162 | 318 | 202 |
| Pamplona | 288 | 0 | 752 | 440 | 92 | 268 |
| Pontevedra | 463 | 752 | 0 | 448 | 781 | 667 |
| Salamanca | 162 | 440 | 448 | 0 | 469 | 364 |
| San Sebastián | 318 | 92 | 781 | 469 | 0 | 228 |
| Santander | 202 | 268 | 667 | 364 | 228 | 0 |
| Segovia | 158 | 370 | 569 | 164 | 429 | 359 |
| Sevilla | 636 | 945 | 922 | 474 | 1007 | 837 |
| Soria | 213 | 176 | 675 | 325 | 268 | 297 |
| Tarragona | 605 | 373 | 1065 | 714 | 465 | 629 |
| Teruel | 444 | 356 | 907 | 514 | 449 | 528 |
| Toledo | 305 | 478 | 682 | 234 | 540 | 464 |
| Valencia | 592 | 501 | 975 | 564 | 594 | 673 |
| Valladolid | 48 | 326 | 459 | 116 | 353 | 249 |
| Vitoria | 200 | 93 | 663 | 351 | 118 | 174 |
| Zamora | 143 | 421 | 386 | 62 | 450 | 344 |
| Zaragoza | 373 | 175 | 833 | 482 | 268 | 397 |
| Palencia | Pamplona | Pontevedra | Salamanca | San Sebastián | Santander |
| Segovia | Sevilla | Soria | Tarragona | Teruel | Toledo | |
| Albacete | 338 | 492 | 473 | 442 | 242 | 240 |
| Alicante | 509 | 609 | 548 | 418 | 317 | 411 |
| Almería | 650 | 422 | 794 | 712 | 577 | 526 |
| Ávila | 67 | 493 | 261 | 648 | 417 | 137 |
| Badajoz | 385 | 217 | 579 | 936 | 703 | 368 |
| Barcelona | 650 | 1046 | 453 | 99 | 409 | 692 |
| Bilbao | 355 | 933 | 257 | 556 | 488 | 466 |
| Burgos | 197 | 775 | 141 | 519 | 372 | 308 |
| Cáceres | 296 | 264 | 490 | 832 | 599 | 264 |
| Cádiz | 750 | 125 | 894 | 1060 | 873 | 583 |
| Castellón | 504 | 762 | 383 | 187 | 152 | 437 |
| Ciudad Real | 277 | 339 | 421 | 648 | 397 | 119 |
| Córdoba | 497 | 138 | 631 | 795 | 596 | 320 |
| Cuenca | 254 | 583 | 359 | 463 | 153 | 187 |
| Gerona | 750 | 1146 | 553 | 197 | 509 | 792 |
| Granada | 521 | 256 | 665 | 771 | 605 | 397 |
| Guadalajara | 145 | 596 | 173 | 475 | 244 | 129 |
| Huelva | 619 | 94 | 863 | 1030 | 842 | 552 |
| Huesca | 426 | 935 | 229 | 210 | 253 | 468 |
| Jaén | 422 | 242 | 566 | 708 | 506 | 298 |
| La Coruña | 560 | 947 | 676 | 1065 | 907 | 675 |
| León | 245 | 671 | 342 | 718 | 573 | 392 |
| Lérida | 494 | 1003 | 297 | 92 | 319 | 536 |
| Logroño | 299 | 874 | 105 | 402 | 336 | 407 |
| Lugo | 462 | 849 | 578 | 967 | 809 | 577 |
| Madrid | 87 | 538 | 231 | 535 | 302 | 71 |
| Málaga | 631 | 219 | 775 | 898 | 715 | 507 |
| Murcia | 488 | 534 | 589 | 493 | 358 | 390 |
| Orense | 467 | 820 | 574 | 963 | 805 | 580 |
| Oviedo | 363 | 789 | 463 | 836 | 694 | 510 |
| Palencia | 158 | 636 | 213 | 605 | 444 | 305 |
| Pamplona | 370 | 945 | 176 | 373 | 356 | 478 |
| Pontevedra | 569 | 922 | 675 | 1065 | 907 | 682 |
| Salamanca | 164 | 474 | 325 | 714 | 514 | 234 |
| San Sebastián | 429 | 1007 | 268 | 465 | 449 | 540 |
| Santander | 359 | 837 | 297 | 629 | 528 | 464 |
| Segovia | 0 | 560 | 194 | 586 | 389 | 158 |
| Sevilla | 560 | 0 | 769 | 948 | 748 | 458 |
| Soria | 194 | 769 | 0 | 387 | 231 | 302 |
| Tarragona | 586 | 948 | 387 | 0 | 311 | 605 |
| Teruel | 389 | 748 | 231 | 311 | 0 | 340 |
| Toledo | 158 | 458 | 302 | 605 | 340 | 0 |
| Valencia | 439 | 697 | 376 | 251 | 145 | 372 |
| Valladolid | 112 | 588 | 211 | 597 | 442 | 259 |
| Vitoria | 311 | 825 | 191 | 489 | 422 | 422 |
| Zamora | 182 | 536 | 306 | 694 | 537 | 296 |
| Zaragoza | 354 | 863 | 157 | 231 | 181 | 396 |
| Segovia | Sevilla | Soria | Tarragona | Teruel | Toledo |
| Valencia | Valladolid | Vitoria | Zamora | Zaragoza | |
| Albacete | 191 | 445 | 602 | 499 | 423 |
| Alicante | 166 | 616 | 739 | 670 | 498 |
| Almería | 460 | 757 | 914 | 811 | 758 |
| Ávila | 467 | 122 | 357 | 159 | 418 |
| Badajoz | 716 | 415 | 650 | 361 | 726 |
| Barcelona | 349 | 664 | 530 | 759 | 296 |
| Bilbao | 633 | 281 | 66 | 376 | 324 |
| Burgos | 517 | 123 | 114 | 218 | 287 |
| Cáceres | 636 | 326 | 561 | 272 | 622 |
| Cádiz | 808 | 715 | 1014 | 661 | 988 |
| Castellón | 65 | 564 | 574 | 665 | 283 |
| Ciudad Real | 398 | 378 | 541 | 415 | 515 |
| Córdoba | 545 | 579 | 751 | 616 | 725 |
| Cuenca | 220 | 361 | 518 | 415 | 334 |
| Gerona | 449 | 764 | 630 | 859 | 396 |
| Granada | 519 | 628 | 785 | 682 | 759 |
| Guadalajara | 410 | 252 | 352 | 306 | 267 |
| Huelva | 791 | 649 | 919 | 595 | 957 |
| Huesca | 398 | 438 | 256 | 535 | 72 |
| Jaén | 455 | 529 | 686 | 583 | 660 |
| La Coruña | 961 | 456 | 549 | 411 | 833 |
| León | 685 | 135 | 315 | 135 | 488 |
| Lérida | 324 | 508 | 374 | 603 | 140 |
| Logroño | 481 | 238 | 86 | 333 | 172 |
| Lugo | 863 | 356 | 451 | 313 | 735 |
| Madrid | 352 | 194 | 351 | 248 | 325 |
| Málaga | 648 | 738 | 895 | 792 | 869 |
| Murcia | 241 | 595 | 752 | 649 | 539 |
| Orense | 873 | 357 | 561 | 284 | 731 |
| Oviedo | 803 | 253 | 340 | 253 | 604 |
| Palencia | 592 | 48 | 200 | 143 | 373 |
| Pamplona | 501 | 326 | 93 | 421 | 175 |
| Pontevedra | 975 | 459 | 663 | 386 | 833 |
| Salamanca | 564 | 116 | 351 | 62 | 482 |
| San Sebastián | 594 | 353 | 118 | 450 | 268 |
| Santander | 673 | 249 | 174 | 344 | 397 |
| Segovia | 439 | 112 | 311 | 182 | 354 |
| Sevilla | 697 | 588 | 825 | 536 | 863 |
| Soria | 376 | 211 | 191 | 306 | 157 |
| Tarragona | 251 | 597 | 489 | 694 | 231 |
| Teruel | 145 | 442 | 422 | 537 | 181 |
| Toledo | 372 | 259 | 422 | 296 | 396 |
| Valencia | 0 | 546 | 576 | 600 | 326 |
| Valladolid | 546 | 0 | 236 | 96 | 367 |
| Vitoria | 576 | 236 | 0 | 332 | 258 |
| Zamora | 600 | 96 | 332 | 0 | 463 |
| Zaragoza | 326 | 367 | 258 | 463 | 0 |
| Valencia | Valladolid | Vitoria | Zamora | Zaragoza |
| Red Radio de Emergencia - R E M E R - | DGPCE |